Câu hỏi:
2 năm trước
Cho tam giác \(MNP\) có \(MN = 5cm,NP = 12cm,MP = 13cm\). Vẽ đường tròn \(\left( {M;NM} \right)\). Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
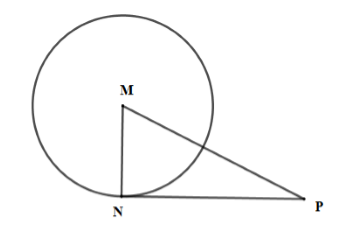
+) Xét tam giác \(MNP\) có \(M{P^2} = {13^2} = 169;N{M^2} + N{P^2} = {5^2} + {12^2} = 169\)\( \Rightarrow M{P^2} = N{M^2} + N{P^2}\)
\( \Rightarrow \Delta MNP\) vuông tại N (định lý Pytago đảo)
\( \Rightarrow MN \bot NP\) mà \(N \in \left( {M;MN} \right)\) nên \(NP\) là tiếp tuyến của \(\left( {M;MN} \right)\)
Hướng dẫn giải:
Sử dụng cách chứng minh tiếp tuyến
Để chứng minh đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\) tại tiếp điểm là \(M\) ta chứng minh \(OM \bot d\) tại \(M\) và \(M \in \left( O \right)\).
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
