Cho hình chữ nhật ABCD, H là hình chiếu của A lên BD. M, N lần lượt là trung điểm của BH, CD. Đường nào sau đây là tiếp tuyến của đường tròn tâm A, bán kính AM.
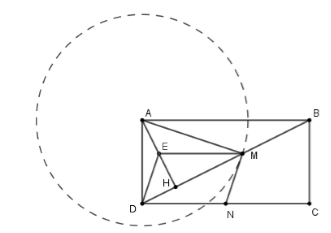
Lấy E là trung điểm của AH. Do M là trung điểm của BH (gt) nên EM là đường trung bình của \(\Delta AHB\) \( \Rightarrow {\rm{ }}EM{\rm{ }}//{\rm{ }}AB\) và \(EM = \dfrac{1}{2}\;AB.\)
Hình chữ nhật ABCD có CD // AB và CD = AB mà N là trung điểm của DC, suy ra
\(DN//AB\) và \(DN = \;\dfrac{1}{2}AB.\)
Từ (1) và (2) ta có EM // DN và EM = DN
Suy ra tứ giác EMND là hình bình hành, do đó DN // EM.
Mà \(DN{\rm{ }} \bot AD\)=>\(EM{\rm{ }} \bot AD\) (tính chất hình chữ nhật)
\(AH \bot DM\) (gt) nên E là trực tâm của ∆ADM
Suy ra \(DE \bot AM,\) mà DE // MN (cmt)
\( \Rightarrow MN\; \bot AM\) tại M.
Vì vậy MN là tiếp tuyến của đường tròn (A ; AM).
Chọn câu đúng.
Vì tứ giác AHGE là hình thoi (theo câu trước) nên AH // GE (1) và \(HE \bot AG\) (tính chất) nên \(\widehat {ADB} = 90^\circ \) (do đó C đúng)
Xét \(\Delta ABG\) có BD và AC là đường cao, mà BD cắt AC tại E
Suy ra E là trực tâm của \(\Delta ABG\), do đó \(GE\; \bot AB.\;\;\) (2)
Từ (1) và (2) suy ra \(AH \bot AB\)
Do đó AH là tiếp tuyến của đường tròn đường kính AB.
Gọi $M$ là trung điểm $BC$. Đường tròn $\left( F \right)$ ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến
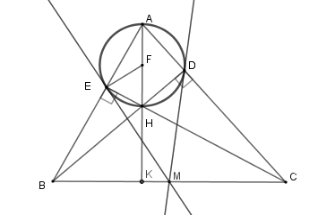
$AH$ cắt $BC$ tại $K$$ \Rightarrow AK \bot BC$ vì $H$ là trực tâm tam giác $ABC$
Ta chứng minh $ME \bot \,EF$ tại $E$.
$\Delta FAE$ cân tại $F$ (vì $FA = FE$) nên $\widehat {FEA} = \widehat {FAE}$
$\Delta MEC$ cân tại $M$ (vì $ME = MC = MB = \dfrac{{BC}}{2}$) nên $\widehat {MEC} = \widehat {MCE}$ mà $\widehat {BAK} = \widehat {ECB}$ (cùng phụ với $\widehat {ABC}$)
nên $\widehat {MEC} = \widehat {FEA}$$ \Rightarrow \widehat {MEC} + \widehat {FEC} = \widehat {FEA} + \widehat {FEC} \Rightarrow \widehat {MEF} = 90^\circ \Rightarrow $$ME \bot \,EF$ tại $E$.
Từ đó $ME$ là tiếp tuyến của $\left( {F;\dfrac{{AH}}{2}} \right)$.
Tương tự ta cũng có $MD$ là tiếp tuyến của $\left( {F;\dfrac{{AH}}{2}} \right)$.
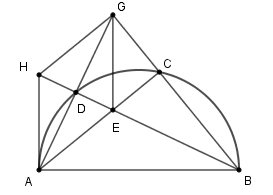
Chọn đáp án đúng nhất. Tứ giác AHGE là hình gì ?
Vì D thuộc đường tròn đường kính AB nên \(BD \bot AD{\rm{ }} \Rightarrow {\rm{ }}BD\) là đường cao của \(\Delta ABG,\) mà BD là đường phân giác của ABG (gt) nên BD vừa là đường cao vừa là đường phân giác của \(\Delta ABG\)
Do đó \(\Delta ABG\) cân tại B suy ra BD là trung trực của AG. (1)
Vì H đối xứng với E qua D (gt) nên D là trung điểm của HE. (2)
Từ (1) và (2) suy ra D là trung điểm của HE và AG
Do đó tứ giác AHGE là hình bình hành (dấu hiệu nhận biết hình bình hành).
Mà \(HE \bot AG\) nên \(\Delta HGE\) là hình thoi (dấu hiệu nhận biết hình thoi).
Xác định tâm $F$ của đường tròn đi qua bốn điểm $A,D,H,E$.
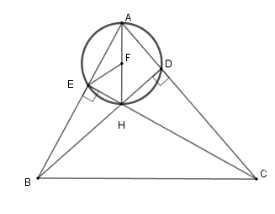
Gọi $F$ là trung điểm của $AH$
Xét hai tam giác vuông $AEH$ và $ADH$ ta có $FA = FH = FE = FD = \dfrac{{AH}}{2}$
Nên bốn đỉnh $A,D,H,E$ cùng thuộc đường tròn tâm $F$ bán kính $\dfrac{{AH}}{2}$.
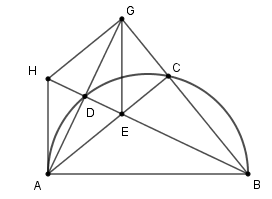
Chọn đáp án đúng nhất. Tứ giác AHGE là hình gì ?

Vì D thuộc đường tròn đường kính AB nên \(BD \bot AD{\rm{ }} \Rightarrow {\rm{ }}BD\) là đường cao của \(\Delta ABG,\) mà BD là đường phân giác của ABG (gt) nên BD vừa là đường cao vừa là đường phân giác của \(\Delta ABG\)
Do đó \(\Delta ABG\) cân tại B suy ra BD là trung trực của AG. (1)
Vì H đối xứng với E qua D (gt) nên D là trung điểm của HE. (2)
Từ (1) và (2) suy ra D là trung điểm của HE và AG
Do đó tứ giác AHGE là hình bình hành (dấu hiệu nhận biết hình bình hành).
Mà \(HE \bot AG\) nên \(\Delta HGE\) là hình thoi (dấu hiệu nhận biết hình thoi).
Xác định tâm $F$ của đường tròn đi qua bốn điểm $A,D,H,E$.

Gọi $F$ là trung điểm của $AH$
Xét hai tam giác vuông $AEH$ và $ADH$ ta có $FA = FH = FE = FD = \dfrac{{AH}}{2}$
Nên bốn đỉnh $A,D,H,E$ cùng thuộc đường tròn tâm $F$ bán kính $\dfrac{{AH}}{2}$.
Cho bán kính của đường tròn bằng \(10\,cm\); \(MN = 12cm\). Tính \(OP.\)
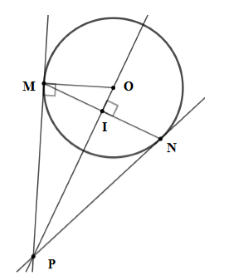
Gọi \(I\) là giao điểm của \(MN\) và \(OP\)
Ta có: \(OP \bot MN\) tại \(I\) \( \Rightarrow \) \(I\) là trung điểm của MN.
Nên \(IM = \dfrac{{MN}}{2} = \dfrac{{12}}{2} = 6\,cm\)
Xét tam giác vuông \(OMI\) có \(OI = \sqrt {O{M^2} - M{I^2}} = \sqrt {{{10}^2} - {6^2}} = 8\,cm\)
Xét tam giác vuông \(MPO\), theo hệ thức lượng trong tam giác vuôg ta có \(M{O^2} = OI.OP \Rightarrow OP = \dfrac{{M{O^2}}}{{OI}} = \dfrac{{{{10}^2}}}{8} = 12,5\,cm\)
Vậy \(OP = 12,5\,cm\).
Chọn khẳng định đúng?
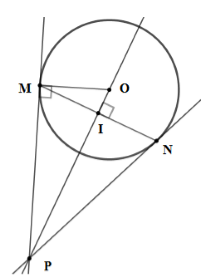
Gọi \(I\) là giao điểm của \(MN\) và \(OP\)
Ta có: \(OP \bot MN\) tại \(I\) \( \Rightarrow \) \(I\) là trung điểm của MN.
\( \Rightarrow \)\(PI\) là đường cao đồng thời là trung tuyến của \(\Delta MNP\).
\( \Rightarrow \)\(\Delta MNP\) cân tại \(P\).
\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat {MPO} = \widehat {NPO}\\PM = PN\end{array} \right.\)\( \Rightarrow \Delta PMO = \Delta PNO\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {PMO} = \widehat {PNO} = 90^\circ \Rightarrow ON \bot NP\)
\( \Rightarrow \)\(PN\) là tiếp tuyến của \(\left( O \right)\)
Chọn khẳng định đúng?

Gọi \(I\) là giao điểm của \(MN\) và \(OP\)
Ta có: \(OP \bot MN\) tại \(I\) \( \Rightarrow \) \(I\) là trung điểm của MN.
\( \Rightarrow \)\(PI\) là đường cao đồng thời là trung tuyến của \(\Delta MNP\).
\( \Rightarrow \)\(\Delta MNP\) cân tại \(P\).
\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat {MPO} = \widehat {NPO}\\PM = PN\end{array} \right.\)\( \Rightarrow \Delta PMO = \Delta PNO\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {PMO} = \widehat {PNO} = 90^\circ \Rightarrow ON \bot NP\)
\( \Rightarrow \)\(PN\) là tiếp tuyến của \(\left( O \right)\)
Tính độ dài \(MC\).
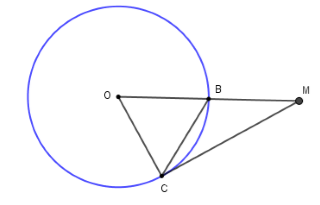
Theo câu trước ta có \(\Delta OCM\) vuông tại \(C\)
Áp dụng định lý Pytago cho tam giác vuông \(OCM\), ta có \(O{M^2} = O{C^2} + M{C^2}\)\( \Rightarrow M{C^2} = O{M^2} - O{C^2} \)\(= {4^2} - {2^2} = 12 \Rightarrow MC = 2\sqrt 3 \,cm\)
Chọn khẳng định đúng ?
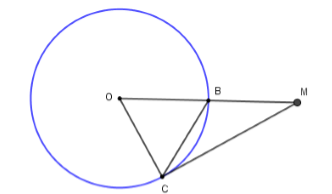
Tam giác \(OBC\) cân tại \(O\) có \(\widehat {OBC} = 60^\circ \)
Nên tam giác \(OCB\) là tam giác đều suy ra \(BC = OB = OC = 2\)
Xét tam giác \(OCM\) có \(BC = OB = BM = 2 = \dfrac{{OM}}{2}\) nên \(\Delta OCM\) vuông tại \(C\)
\( \Rightarrow OC \bot CM \Rightarrow MC\) là tiếp tuyến của \((O;2cm).\)
Chọn khẳng định đúng ?

Tam giác \(OBC\) cân tại \(O\) có \(\widehat {OBC} = 60^\circ \)
Nên tam giác \(OCB\) là tam giác đều suy ra \(BC = OB = OC = 2\)
Xét tam giác \(OCM\) có \(BC = OB = BM = 2 = \dfrac{{OM}}{2}\) nên \(\Delta OCM\) vuông tại \(C\)
\( \Rightarrow OC \bot CM \Rightarrow MC\) là tiếp tuyến của \((O;2cm).\)
Độ dài tiếp tuyến $AB$ là
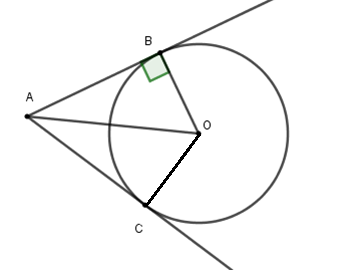
Từ hình vẽ ta có $AB;AC$ là tiếp tuyến của $\left( O \right)$ tại $B,C$ suy ra $OC \bot AC$ tại $C$.
Suy ra $\Delta ABO = \Delta ACO\left( {c - g - c} \right)$ nên $\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 30^\circ $
Xét $\Delta ABO$ có $AB = AO.\cos A = 10.\cos 30^\circ = 5\sqrt 3 $.
Độ dài bán kính $OB$ là
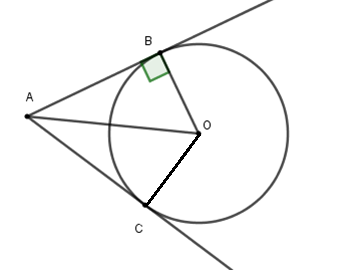
Từ hình vẽ ta có $AB;AC$ là tiếp tuyến của $\left( O \right)$ tại $B,C$ suy ra $OC \bot AC$ tại $C$.
Suy ra $\Delta ABO = \Delta ACO\left( {c - g - c} \right)$ nên $\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 30^\circ $
Xét $\Delta ABO$ có $OB = AO.\sin A = 10.\sin 30^\circ = 5\,cm$
Độ dài bán kính $OB$ là

Từ hình vẽ ta có $AB;AC$ là tiếp tuyến của $\left( O \right)$ tại $B,C$ suy ra $OC \bot AC$ tại $C$.
Suy ra $\Delta ABO = \Delta ACO\left( {c - g - c} \right)$ nên $\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 30^\circ $
Xét $\Delta ABO$ có $OB = AO.\sin A = 10.\sin 30^\circ = 5\,cm$
Cho $\left( {O;R} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm $A$ khi
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Cho $\left( {O;5cm} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;5\,cm} \right)$, khi đó
Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bán kính của đường tròn đó.
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
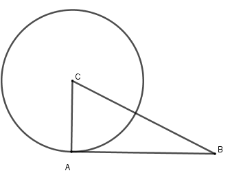
+) Xét tam giác $ABC$ có \(B{C^2} = {5^2} = 25;A{B^2} + A{C^2} = {4^2} + {3^2} = 25; \Rightarrow B{C^2} = A{B^2} + A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại A (định lý Pytago đảo)
\( \Rightarrow AB \bot AC\) mà $A \in \left( {C;CA} \right)$ nên $AB$ là tiếp tuyến của $\left( {C;CA} \right)$
Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
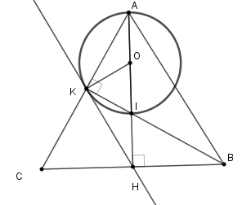
Gọi $O$ là trung điểm $AI$. Xét tam giác vuông $AIK$ có $OK = OI = OA \Rightarrow K \in \left( {O;\dfrac{{AI}}{2}} \right)$ (*)
Ta đi chứng minh $OK \bot KH$ tại $K$.
Xét tam giác $OKA$ cân tại $O$ ta có $\widehat {OKA} = \widehat {OAK}$ $\left( 1 \right)$
Vì tam giác $ABC$ cân tại $A$ có đường cao $AH$ nên $H$ là trung điểm của$BC$ . Xét tam giác vuông $BKC$ có $HK = HB = HC = \dfrac{{BC}}{2}$
Suy ra tam giác $KHB$ cân tại $H$ nên $\widehat {HKB} = \widehat {HBK}$$\left( 2 \right)$
Mà $\widehat {HBK} = \widehat {KAH}$ (cùng phụ với $\widehat {ACB}$) $\left( 3 \right)$
Từ $\left( 1 \right);\left( 2 \right);\left( 3 \right)$ suy ra $\widehat {HKB} = \widehat {AKO}$ mà $\widehat {AKO} + \widehat {OKI} = 90^\circ \Rightarrow \widehat {HKB} + \widehat {OKI} = 90^\circ \Rightarrow \widehat {OKH} = 90^\circ $ hay $OK \bot KH$ tại $K$ (**)
Từ (*) và (**) thì $HK$ là tiếp tuyến của đường tròn đường kính $AI$.

