Cho hình chữ nhật ABCD, H là hình chiếu của A lên BD. M, N lần lượt là trung điểm của BH, CD. Đường nào sau đây là tiếp tuyến của đường tròn tâm A, bán kính AM.

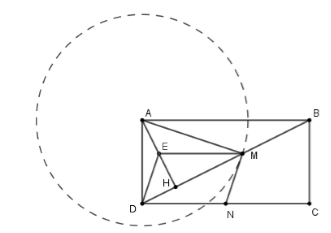
Lấy E là trung điểm của AH. Do M là trung điểm của BH (gt) nên EM là đường trung bình của \(\Delta AHB\) \( \Rightarrow {\rm{ }}EM{\rm{ }}//{\rm{ }}AB\) và \(EM = \dfrac{1}{2}\;AB.\)

Hình chữ nhật ABCD có CD // AB và CD = AB mà N là trung điểm của DC, suy ra

\(DN//AB\) và \(DN = \;\dfrac{1}{2}AB.\)

Từ (1) và (2) ta có EM // DN và EM = DN

Suy ra tứ giác EMND là hình bình hành, do đó DN // EM.

Mà \(DN{\rm{ }} \bot AD\)=>\(EM{\rm{ }} \bot AD\)  (tính chất hình chữ nhật)

\(AH \bot DM\)  (gt) nên E là trực tâm của ∆ADM

Suy ra \(DE \bot AM,\) mà DE // MN (cmt)

 \( \Rightarrow MN\; \bot AM\) tại M.

Vì vậy MN là tiếp tuyến của đường tròn (A ; AM).