Trả lời bởi giáo viên
Đáp án đúng: a
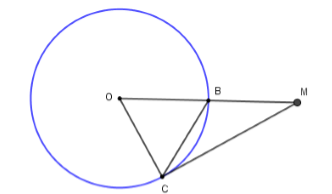
Tam giác \(OBC\) cân tại \(O\) có \(\widehat {OBC} = 60^\circ \)
Nên tam giác \(OCB\) là tam giác đều suy ra \(BC = OB = OC = 2\)
Xét tam giác \(OCM\) có \(BC = OB = BM = 2 = \dfrac{{OM}}{2}\) nên \(\Delta OCM\) vuông tại \(C\)
\( \Rightarrow OC \bot CM \Rightarrow MC\) là tiếp tuyến của \((O;2cm).\)
Hướng dẫn giải:
Sử dụng cách chứng minh đường thẳng là tiếp tuyến
Sử dụng: “ Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông”
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
