Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
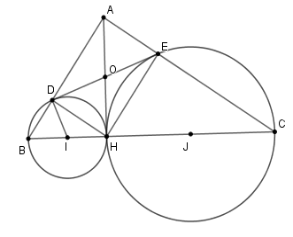
Gọi $I$, $J$ lần lượt là trung điểm của $BH$ và $CH.$
Để chứng minh $DE$ là tiếp tuyến của đường tròn tâm $I$ đường kính $BH$ ta chứng minh
\(ID \bot DE\) hay $\widehat {ODI} = {90^o}$
Vì $D,E$ lần lượt thuộc đường tròn đường kính $BH$ và $HC$ nên ta có: $\widehat {BDH} = \widehat {CEH} = {90^0}$
Suy ra tứ giác $ADHE$ là hình chữ nhật.
Gọi $O$ là giao điểm của $AH$ và$DE$, khi đó ta có $OD = OH = OE = OA$ .
Suy ra $\Delta ODH$ cân tại $O \Rightarrow \widehat {ODH} = \widehat {OHD}$
Ta cũng có $\Delta IDH$ cân tại $I$$ \Rightarrow \widehat {IDH} = \widehat {IHD}$
Từ đó $ \Rightarrow \widehat {IDH} + \widehat {HDO} = \widehat {IHD} + \widehat {DHO} \Rightarrow \widehat {IDO} = 90^\circ $$ \Rightarrow ID \bot DE$
Ta có \(ID \bot DE,D \in \left( I \right)\) nên $DE$ là tiếp tuyến của đường tròn đường kính $BH$.
Từ chứng minh trên suy ra các phương án B,C,D đúng.
Cho đường tròn $(O;R)$ đường kính $AB$. Vẽ dây $AC$ sao cho \(\widehat {ABC} = 30^\circ \) . Trên tia đối của tia $AB$ lấy điểm $M$ sao cho $AM = R$ .
Chọn khẳng định đúng?
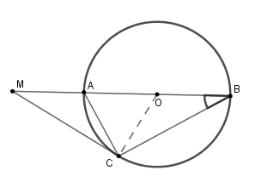
Tam giác $OBC$ cân tại $O$ có \(\widehat {ABC} = 30^\circ \) suy ra $\widehat {AOC} = 60^\circ $ (góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với nó).
Nên tam giác $OCA$ là tam giác đều suy ra \(AC = AO = AM = R.\) \( \Rightarrow \widehat {OCM} = {90^ \circ } \Rightarrow MC\) là tiếp tuyến của \((O;R).\)
Cho đường tròn $(O;R)$ đường kính $AB$. Vẽ dây $AC$ sao cho \(\widehat {ABC} = 30^\circ \) . Trên tia đối của tia $AB$ lấy điểm $M$ sao cho $AM = R$ .
Tính độ dài $MC$ theo $R.$
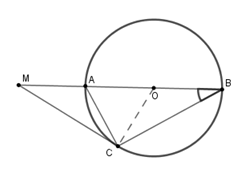
Áp dụng định lý Pytago cho tam giác vuông $OCM$, ta có \(O{M^2} = O{C^2} + M{C^2}\)\( \Rightarrow M{C^2} = O{M^2} - O{C^2} = 3{R^2} \Rightarrow MC = \sqrt 3 R.\)
Từ một điểm $A$ ở bên ngoài đường tròn $\left( {O;R} \right)$,vẽ hai tiếp tuyến $AB,AC$ với $\left( O \right)$. Đường thẳng vuông góc với $OB$ tại $O$ cắt tia $AC$ tại $N$. Đường thẳng vuông góc với $OC$ tại $O$ cắt tia $AB$ tại $M$.
Tứ giác $AMON$ là hình gì?
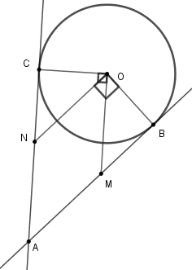
Dễ có $AMON$ là hình bình hành (Vì $ON{\rm{//}}AM;OM{\rm{//}}AN$).
Ta chứng minh \(OM = ON\).
Xét tam giác $OBM$ và tam giác $OCN$ có :
\(\widehat {OBM} = \widehat {OCN} = {90^0};\)
\({\rm{ }}OB = OC = R,\)
và \(\widehat {OMB} = \widehat {ONC} = \widehat A \)
\(\Rightarrow \Delta OBM = \Delta OCN\)
\( \Rightarrow OM = ON \Rightarrow AMON\) là hình thoi .
Từ một điểm $A$ ở bên ngoài đường tròn $\left( {O;R} \right)$,vẽ hai tiếp tuyến $AB,AC$ với $\left( O \right)$. Đường thẳng vuông góc với $OB$ tại $O$ cắt tia $AC$ tại $N$. Đường thẳng vuông góc với $OC$ tại $O$ cắt tia $AB$ tại $M$.
Điểm $A$ phải cách $O$ một khoảng là bao nhiêu để cho $MN$ là tiếp tuyến của $\left( O \right)$?
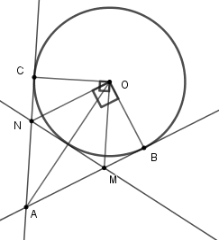
Tứ giác $AMON$ là hình thoi nên \(OA \bot MN\) và
Mà độ dài $OA$ bằng $2$ lần khoảng cách từ $O$ đến$MN$ .
Do đó $MN$ là tiếp tuyến đường tròn \(\left( {O;{\rm{ R}}} \right) \Leftrightarrow \) khoảng cách từ $O$ đến $MN$ bằng R \( \Leftrightarrow OA = 2R\).
Cho đường tròn$\left( O \right)$ , dây $AB$ khác đường kính. Qua $O$ kẻ đường vuông góc với $AB$ , cắt tiếp tuyến tại $A$ của đường tròn ở điểm $C$ .
Chọn khẳng định đúng?
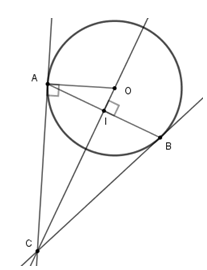
Ta có: \(OC \bot AB\) \( \Rightarrow \) $OC$ đi qua trung điểm của $AB$.
\( \Rightarrow \)$OC$ là đường cao đồng thời là trung tuyến của\(\Delta ABC\).
\( \Rightarrow \)\(\Delta ABC\) cân tại $C$.
\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat {ACO} = \widehat {BCO}\\AC = CB\end{array} \right.\)\( \Rightarrow \Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow OB \bot BC\)
\( \Rightarrow \)$BC$ là tiếp tuyến của $\left( O \right)$
Cho đường tròn$\left( O \right)$ , dây $AB$ khác đường kính. Qua $O$ kẻ đường vuông góc với $AB$ , cắt tiếp tuyến tại $A$ của đường tròn ở điểm $C$ .
Cho bán kính của đường tròn bằng $15\,cm$; $AB = 24cm$. Tính $OC$
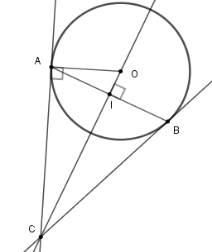
Gọi $I$ là giao điểm của $OC$ và$AB \Rightarrow AI = BI = \dfrac{{AB}}{2} = 12\,cm$
Xét tam giác vuông $OAI$ có $OI = \sqrt {O{A^2} - A{I^2}} = 9\,cm$
Xét tam giác vuông $AOC$ có $A{O^2} = OI.OC \Rightarrow OC = \dfrac{{A{O^2}}}{{OI}} = \dfrac{{{{15}^2}}}{9} = 25\,cm$
Vậy $OC = 25\,cm$.
Cho tam giác $ABC$ có hai đường cao $BD,CE$ cắt nhau tại $H$.
Xác định tâm $F$ của đường tròn đi qua bốn điểm $A,D,H,E$.
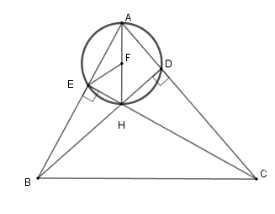
Gọi $F$ là trung điểm của $AH$
Xét hai tam giác vuông $AEH$ và $ADH$ ta có $FA = FH = FE = FD = \dfrac{{AH}}{2}$
Nên bốn đỉnh $A,D,H,E$ cùng thuộc đường tròn tâm $F$ bán kính $\dfrac{{AH}}{2}$.
Cho tam giác $ABC$ có hai đường cao $BD,CE$ cắt nhau tại $H$.
Gọi $M$ là trung điểm $BC$. Đường tròn $\left( F \right)$ ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến
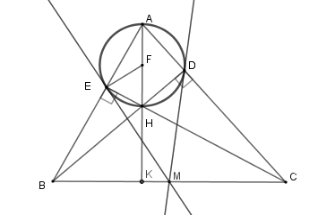
$AH$ cắt $BC$ tại $K$$ \Rightarrow AK \bot BC$ vì $H$ là trực tâm tam giác $ABC$
Ta chứng minh $ME \bot \,EF$ tại $E$.
$\Delta FAE$ cân tại $F$ (vì $FA = FE$) nên $\widehat {FEA} = \widehat {FAE}$
$\Delta MEC$ cân tại $M$ (vì $ME = MC = MB = \dfrac{{BC}}{2}$) nên $\widehat {MEC} = \widehat {MCE}$ mà $\widehat {BAK} = \widehat {ECB}$ (cùng phụ với $\widehat {ABC}$)
nên $\widehat {MEC} = \widehat {FEA}$$ \Rightarrow \widehat {MEC} + \widehat {FEC} = \widehat {FEA} + \widehat {FEC} \Rightarrow \widehat {MEF} = 90^\circ \Rightarrow $$ME \bot \,EF$ tại $E$.
Từ đó $ME$ là tiếp tuyến của $\left( {F;\dfrac{{AH}}{2}} \right)$.
Tương tự ta cũng có $MD$ là tiếp tuyến của $\left( {F;\dfrac{{AH}}{2}} \right)$.
Cho hình vẽ dưới đây. Biết \(\widehat {BAC} = {60^0};AO = 10\,cm\). Chọn đáp án đúng.
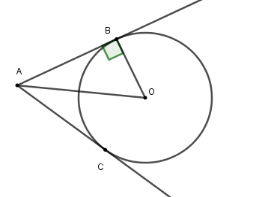
Độ dài bán kính $OB$ là
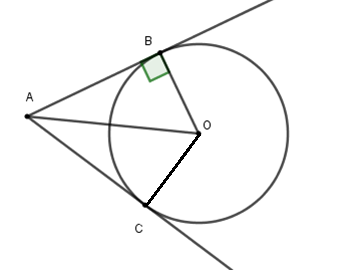
Từ hình vẽ ta có $AB;AC$ là tiếp tuyến của $\left( O \right)$ tại $B,C$ suy ra $OC \bot AC$ tại $C$.
Suy ra $\Delta ABO = \Delta ACO\left( {c - g - c} \right)$ nên $\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 30^\circ $
Xét $\Delta ABO$ có $OB = AO.\sin A = 10.\sin 30^\circ = 5\,cm$
Cho hình vẽ dưới đây. Biết \(\widehat {BAC} = {60^0};AO = 10\,cm\). Chọn đáp án đúng.

Độ dài tiếp tuyến $AB$ là
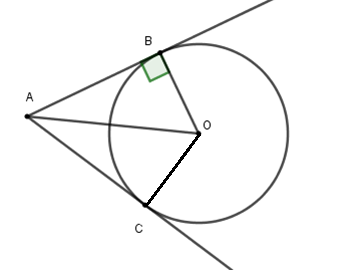
Từ hình vẽ ta có $AB;AC$ là tiếp tuyến của $\left( O \right)$ tại $B,C$ suy ra $OC \bot AC$ tại $C$.
Suy ra $\Delta ABO = \Delta ACO\left( {c - g - c} \right)$ nên $\widehat {BAO} = \widehat {CAO} = \dfrac{{\widehat {BAC}}}{2} = 30^\circ $
Xét $\Delta ABO$ có $AB = AO.\cos A = 10.\cos 30^\circ = 5\sqrt 3 $.
Cho nửa đường tròn (O ; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB lấy điểm D sao cho \(CD = 3R. \) Chọn câu đúng.
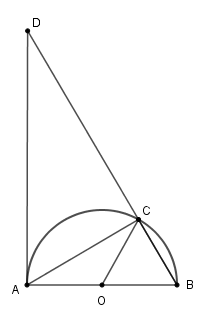
Vì AB là đường kính của (O ; R) nên AB = 2R.
Vì D thuộc tia đối của tia CB nên
\(BD = CD + BC = 3R + R = 4R\) .
Suy ra \(\dfrac{{AB}}{{BD}} = \dfrac{{2R}}{{4R}} = \dfrac{1}{2};\,\dfrac{{BC}}{{AB}} = \dfrac{R}{{2R}} = \dfrac{1}{2}\)
Xét ∆ABD và ∆CBA có \(\widehat B\) chung và \(\dfrac{{BC}}{{AB}} = \dfrac{{AB}}{{BD}} = \dfrac{1}{2}\) (cmt)
Vì vậy \(\Delta ABD \backsim \Delta CBA\) (c.g.c) \( \Rightarrow \widehat {DAB}{\rm{ = }}\widehat {ACB}{\rm{ }}\)
Mà C thuộc (O ; R) và AB là đường kính nên \(OC = OA = OB = \dfrac{{AB}}{2}\) suy ra \(\Delta ACB\) vuông tại \(C\) hay \(\widehat {ACB} = 90^\circ \) . Do đó \(\widehat {DAB}{\rm{ = }}\widehat {ACB} = 90^\circ \) hay \(AD \bot AB\)
Suy ra AD là tiếp tuyến của \(\left( {O;R} \right).\)
Cho \(\widehat {xOy}\) , trên Ox lấy P, trên Oy lấy Q sao cho chu vi ∆POQ bằng 2a không đổi. Chọn câu đúng.
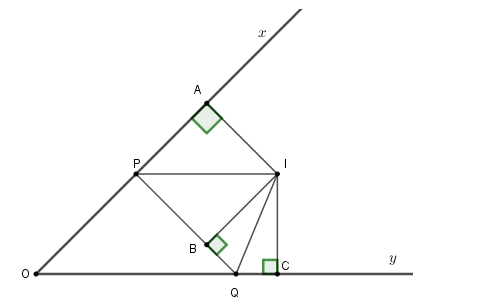
Gọi I là giao điểm các tia phân giác của \(\widehat {xPQ};\,\widehat {yQP}\) và A, B, C lần lượt là hình chiếu của I lên Ox, PQ và Oy.
Vì I thuộc phân giác của góc xPQ nên IA = IB.
Xét ∆PAI và ∆PBI có :
+ IA = IB (cmt)
+ Chung PI
+ \(\widehat {PAI} = \widehat {PBI} = 90^\circ \)
nên ∆PAI = ∆PBI (cạnh huyền – cạnh góc vuông) ,
Suy ra PA = PB.
Lí luận tương tự, ta có \(QB = QC.\)
\(OA + OC = OP + PA + OQ + QC\) \( = OP + PB + OQ + QB = OP + PQ + QO = 2a\) (do chu vi ∆OPQ bằng 2a).
Vì IA = IB và IB = IC (cmt) nên IA = IC.
Xét ∆OAI và ∆OCI có
+ IA = IC (cmt)
+ \(\widehat {OAI} = \widehat {OCI} = 90^\circ \)
+ cạnh chung OI
nên ∆OAI = ∆OCI (cạnh huyền – cạnh góc vuông) \( \Rightarrow OA = OC = \dfrac{{2a}}{2} = a{\rm{ }}.\)
Vì a không đổi và A, C thuộc tia Ox, Oy cố định nên A và C cố định.
Do A và C lần lượt là hình chiếu của I lên Ox, Oy nên hai đường thẳng AI và CI cố định hay I cố định.
Do I và A cố định nên độ dài đoạn thẳng AI không đổi.
Do IA = IB (cmt) nên IB là bán kính của đường tròn (I ; IA), mà IB ⊥ PQ tại B nên PQ tiếp xúc với đường tròn (I; IA) cố định.

