Câu hỏi:
2 năm trước
Cho đường tròn $(O;R)$ đường kính $AB$. Vẽ dây $AC$ sao cho \(\widehat {ABC} = 30^\circ \) . Trên tia đối của tia $AB$ lấy điểm $M$ sao cho $AM = R$ .
Chọn khẳng định đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
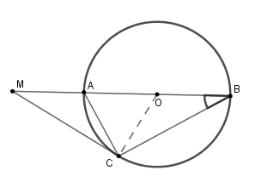
Tam giác $OBC$ cân tại $O$ có \(\widehat {ABC} = 30^\circ \) suy ra $\widehat {AOC} = 60^\circ $ (góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với nó).
Nên tam giác $OCA$ là tam giác đều suy ra \(AC = AO = AM = R.\) \( \Rightarrow \widehat {OCM} = {90^ \circ } \Rightarrow MC\) là tiếp tuyến của \((O;R).\)
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
