Câu hỏi:
2 năm trước
Cho đường tròn$\left( O \right)$ , dây $AB$ khác đường kính. Qua $O$ kẻ đường vuông góc với $AB$ , cắt tiếp tuyến tại $A$ của đường tròn ở điểm $C$ .
Chọn khẳng định đúng?
Trả lời bởi giáo viên
Đáp án đúng: b
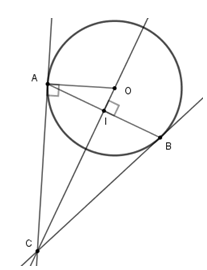
Ta có: \(OC \bot AB\) \( \Rightarrow \) $OC$ đi qua trung điểm của $AB$.
\( \Rightarrow \)$OC$ là đường cao đồng thời là trung tuyến của\(\Delta ABC\).
\( \Rightarrow \)\(\Delta ABC\) cân tại $C$.
\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat {ACO} = \widehat {BCO}\\AC = CB\end{array} \right.\)\( \Rightarrow \Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow OB \bot BC\)
\( \Rightarrow \)$BC$ là tiếp tuyến của $\left( O \right)$
Hướng dẫn giải:
Sử dụng cách chứng minh tiếp tuyến.
Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $M$ ta chứng minh $OM \bot d$ tại $M$ và $M \in \left( O \right)$.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
