Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có hai đường cao $BD,CE$ cắt nhau tại $H$.
Xác định tâm $F$ của đường tròn đi qua bốn điểm $A,D,H,E$.
Trả lời bởi giáo viên
Đáp án đúng: c
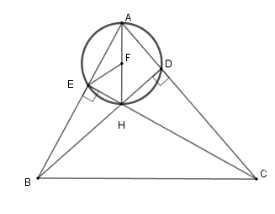
Gọi $F$ là trung điểm của $AH$
Xét hai tam giác vuông $AEH$ và $ADH$ ta có $FA = FH = FE = FD = \dfrac{{AH}}{2}$
Nên bốn đỉnh $A,D,H,E$ cùng thuộc đường tròn tâm $F$ bán kính $\dfrac{{AH}}{2}$.
Hướng dẫn giải:
Xác định điểm cách đều cả bốn điểm cho trước. Điểm đó chính là tâm cần tìm
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
