Cho tam giác $ABC$ có hai đường cao $BD,CE$ cắt nhau tại $H$.

Gọi $M$ là trung điểm $BC$. Đường tròn $\left( F \right)$ ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến

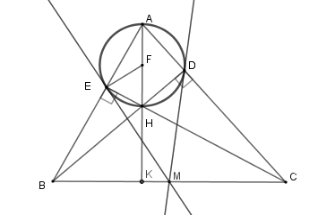
$AH$ cắt $BC$ tại $K$$ \Rightarrow AK \bot BC$ vì $H$ là trực tâm tam giác $ABC$

Ta chứng minh $ME \bot \,EF$ tại $E$.

$\Delta FAE$ cân tại $F$ (vì $FA = FE$) nên $\widehat {FEA} = \widehat {FAE}$

$\Delta MEC$ cân tại $M$ (vì $ME = MC = MB = \dfrac{{BC}}{2}$) nên $\widehat {MEC} = \widehat {MCE}$ mà $\widehat {BAK} = \widehat {ECB}$ (cùng phụ với $\widehat {ABC}$)

 nên $\widehat {MEC} = \widehat {FEA}$$ \Rightarrow \widehat {MEC} + \widehat {FEC} = \widehat {FEA} + \widehat {FEC} \Rightarrow \widehat {MEF} = 90^\circ  \Rightarrow $$ME \bot \,EF$ tại $E$.

Từ đó $ME$ là tiếp tuyến của $\left( {F;\dfrac{{AH}}{2}} \right)$.

Tương tự ta cũng có $MD$ là tiếp tuyến của $\left( {F;\dfrac{{AH}}{2}} \right)$.