Cho nửa đường tròn (O ; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB lấy điểm D sao cho \(CD = 3R. \) Chọn câu đúng.

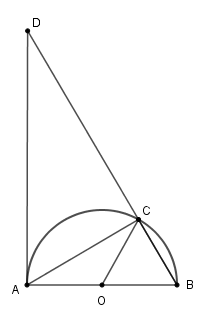
Vì AB là đường kính của (O ; R) nên AB = 2R.

Vì D thuộc tia đối của tia CB nên

\(BD = CD + BC = 3R + R = 4R\) .

Suy ra \(\dfrac{{AB}}{{BD}} = \dfrac{{2R}}{{4R}} = \dfrac{1}{2};\,\dfrac{{BC}}{{AB}} = \dfrac{R}{{2R}} = \dfrac{1}{2}\)

Xét ∆ABD và ∆CBA có \(\widehat B\) chung và \(\dfrac{{BC}}{{AB}} = \dfrac{{AB}}{{BD}} = \dfrac{1}{2}\)  (cmt)

Vì vậy \(\Delta ABD \backsim \Delta CBA\) (c.g.c)  \( \Rightarrow \widehat {DAB}{\rm{ = }}\widehat {ACB}{\rm{ }}\)

Mà C thuộc (O ; R) và AB là đường kính nên \(OC = OA = OB = \dfrac{{AB}}{2}\)  suy ra \(\Delta ACB\) vuông tại \(C\) hay \(\widehat {ACB} = 90^\circ \) . Do đó \(\widehat {DAB}{\rm{ = }}\widehat {ACB} = 90^\circ \) hay \(AD \bot AB\)

Suy ra AD là tiếp tuyến của \(\left( {O;R} \right).\)