Câu hỏi:
2 năm trước
Từ một điểm $A$ ở bên ngoài đường tròn $\left( {O;R} \right)$,vẽ hai tiếp tuyến $AB,AC$ với $\left( O \right)$. Đường thẳng vuông góc với $OB$ tại $O$ cắt tia $AC$ tại $N$. Đường thẳng vuông góc với $OC$ tại $O$ cắt tia $AB$ tại $M$.
Điểm $A$ phải cách $O$ một khoảng là bao nhiêu để cho $MN$ là tiếp tuyến của $\left( O \right)$?
Trả lời bởi giáo viên
Đáp án đúng: a
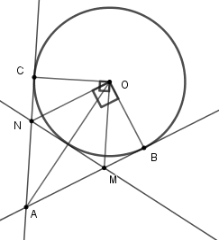
Tứ giác $AMON$ là hình thoi nên \(OA \bot MN\) và
Mà độ dài $OA$ bằng $2$ lần khoảng cách từ $O$ đến$MN$ .
Do đó $MN$ là tiếp tuyến đường tròn \(\left( {O;{\rm{ R}}} \right) \Leftrightarrow \) khoảng cách từ $O$ đến $MN$ bằng R \( \Leftrightarrow OA = 2R\).
Hướng dẫn giải:
Sử dụng tính chất của hình thoi.

