Câu hỏi:
2 năm trước
Cho đường tròn$\left( O \right)$ , dây $AB$ khác đường kính. Qua $O$ kẻ đường vuông góc với $AB$ , cắt tiếp tuyến tại $A$ của đường tròn ở điểm $C$ .
Cho bán kính của đường tròn bằng $15\,cm$; $AB = 24cm$. Tính $OC$
Trả lời bởi giáo viên
Đáp án đúng: c
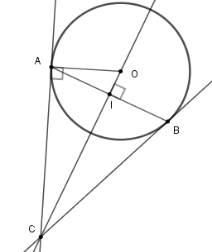
Gọi $I$ là giao điểm của $OC$ và$AB \Rightarrow AI = BI = \dfrac{{AB}}{2} = 12\,cm$
Xét tam giác vuông $OAI$ có $OI = \sqrt {O{A^2} - A{I^2}} = 9\,cm$
Xét tam giác vuông $AOC$ có $A{O^2} = OI.OC \Rightarrow OC = \dfrac{{A{O^2}}}{{OI}} = \dfrac{{{{15}^2}}}{9} = 25\,cm$
Vậy $OC = 25\,cm$.
Hướng dẫn giải:
Sử dụng hệ thức lượng trong tam giác vuông.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
