Câu hỏi:
2 năm trước
Từ một điểm $A$ ở bên ngoài đường tròn $\left( {O;R} \right)$,vẽ hai tiếp tuyến $AB,AC$ với $\left( O \right)$. Đường thẳng vuông góc với $OB$ tại $O$ cắt tia $AC$ tại $N$. Đường thẳng vuông góc với $OC$ tại $O$ cắt tia $AB$ tại $M$.
Tứ giác $AMON$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: b
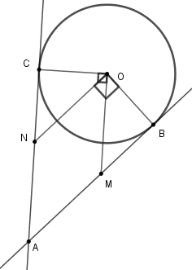
Dễ có $AMON$ là hình bình hành (Vì $ON{\rm{//}}AM;OM{\rm{//}}AN$).
Ta chứng minh \(OM = ON\).
Xét tam giác $OBM$ và tam giác $OCN$ có :
\(\widehat {OBM} = \widehat {OCN} = {90^0};\)
\({\rm{ }}OB = OC = R,\)
và \(\widehat {OMB} = \widehat {ONC} = \widehat A \)
\(\Rightarrow \Delta OBM = \Delta OCN\)
\( \Rightarrow OM = ON \Rightarrow AMON\) là hình thoi .
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết các hình đặc biệt.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
