Trả lời bởi giáo viên
Đáp án đúng: a
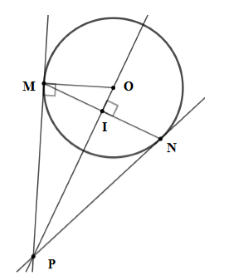
Gọi \(I\) là giao điểm của \(MN\) và \(OP\)
Ta có: \(OP \bot MN\) tại \(I\) \( \Rightarrow \) \(I\) là trung điểm của MN.
Nên \(IM = \dfrac{{MN}}{2} = \dfrac{{12}}{2} = 6\,cm\)
Xét tam giác vuông \(OMI\) có \(OI = \sqrt {O{M^2} - M{I^2}} = \sqrt {{{10}^2} - {6^2}} = 8\,cm\)
Xét tam giác vuông \(MPO\), theo hệ thức lượng trong tam giác vuôg ta có \(M{O^2} = OI.OP \Rightarrow OP = \dfrac{{M{O^2}}}{{OI}} = \dfrac{{{{10}^2}}}{8} = 12,5\,cm\)
Vậy \(OP = 12,5\,cm\).
Hướng dẫn giải:
Sử dụng hệ thức lượng trong tam giác vuông
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
