Trả lời bởi giáo viên
Đáp án đúng: b
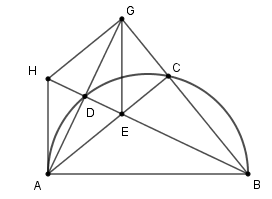
Vì D thuộc đường tròn đường kính AB nên \(BD \bot AD{\rm{ }} \Rightarrow {\rm{ }}BD\) là đường cao của \(\Delta ABG,\) mà BD là đường phân giác của ABG (gt) nên BD vừa là đường cao vừa là đường phân giác của \(\Delta ABG\)
Do đó \(\Delta ABG\) cân tại B suy ra BD là trung trực của AG. (1)
Vì H đối xứng với E qua D (gt) nên D là trung điểm của HE. (2)
Từ (1) và (2) suy ra D là trung điểm của HE và AG
Do đó tứ giác AHGE là hình bình hành (dấu hiệu nhận biết hình bình hành).
Mà \(HE \bot AG\) nên \(\Delta HGE\) là hình thoi (dấu hiệu nhận biết hình thoi).
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết:
Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành
Hình bình hành có một đường chéo vuông góc.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
