Trả lời bởi giáo viên
Đáp án đúng: d
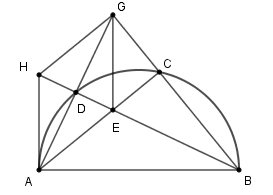
Vì tứ giác AHGE là hình thoi (theo câu trước) nên AH // GE (1) và HE⊥AG (tính chất) nên ^ADB=90∘ (do đó C đúng)
Xét ΔABG có BD và AC là đường cao, mà BD cắt AC tại E
Suy ra E là trực tâm của ΔABG, do đó GE⊥AB. (2)
Từ (1) và (2) suy ra AH⊥AB
Do đó AH là tiếp tuyến của đường tròn đường kính AB.
Hướng dẫn giải:
Sử dụng cách chứng minh tiếp tuyến
Để chứng minh đường thẳng d là tiếp tuyến của đường tròn (O;R) tại tiếp điểm là M ta chứng minh OM⊥d tại M và M∈(O).
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
