Trả lời bởi giáo viên
Đáp án đúng: c
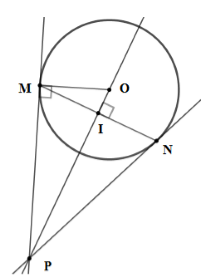
Gọi I là giao điểm của MN và OP
Ta có: OP⊥MN tại I ⇒ I là trung điểm của MN.
⇒PI là đường cao đồng thời là trung tuyến của ΔMNP.
⇒ΔMNP cân tại P.
⇒{^MPO=^NPOPM=PN⇒ΔPMO=ΔPNO(c−g−c)
⇒^PMO=^PNO=90∘⇒ON⊥NP
⇒PN là tiếp tuyến của (O)
Hướng dẫn giải:
Sử dụng cách chứng minh tiếp tuyến
Để chứng minh đường thẳng d là tiếp tuyến của đường tròn (O;R) tại tiếp điểm là M ta chứng minh OM⊥d tại M và M∈(O).
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
