Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$ có $AB = 6cm,{\rm{ }}BC = 10cm,$ đường cao $AH.$ Gọi $E,{\rm{ }}F$ là hình chiếu của $H$ lần lượt lên $AB,{\rm{ }}AC.$
Tính \(EF.\)
Trả lời bởi giáo viên
Đáp án đúng: a
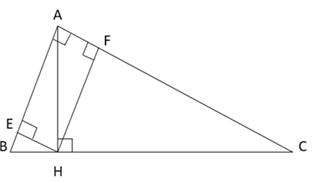
Ta có tam giác $ABC$ vuông tại $A$
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)(cm)
Lại có: $AH$ là đường cao của tam giác vuông $ABC$ nên
\(AH.BC = AB.AC\) (hệ thức lượng trong tam giác vuông)
\( = > AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{6.8}}{{10}} = 4,8\left( {cm} \right)\)
Dễ thấy tứ giác $AFHE$ là hình chữ nhật (có 3 góc vuông)
Nên $EF = AH = 4,8\left( {cm} \right)$
Hướng dẫn giải:
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
