Bài tập hay và khó chương hệ thức lượng trong tam giác vuông

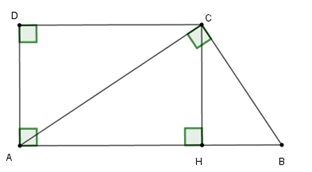
Ta có $\tan \widehat{CAD}=\dfrac{DC}{AD}\Leftrightarrow  AD=DC:\tan 60^0=AD = 10\sqrt 3$ \(\left( {cm} \right)\).

Kẻ \(CH \bot AB\). Tứ giác \(AHCD\) là hình chữ nhật vì có \(\widehat A = \widehat D = \widehat H = {90^0}\), suy ra \(AH = CD = 30cm;CH = AD = 10\sqrt 3 \left( {cm} \right)\).

Tam giác \(ACB\) vuông tại \(C\), ta có: \(C{H^2} = HA.HB\), suy ra \(HB = \dfrac{{C{H^2}}}{{HA}} = \dfrac{{{{\left( {10\sqrt 3 } \right)}^2}}}{{30}} = \dfrac{{300}}{{30}} = 10\left( {cm} \right)\),

do đó \(AB = AH + HB = 30 + 10 = 40\left( {cm} \right).\)

\({S_{ABCD}} = \dfrac{1}{2}CH\left( {AB + CD} \right)=\dfrac{1}{2}.10\sqrt 3 .\left( {40 + 30} \right) = 350\sqrt 3 \left( {c{m^2}} \right).\)

Vậy diện tích hình thang \(ABCD\) bằng \(350\sqrt 3 c{m^2}\)

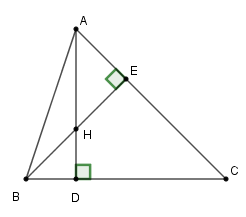
Ta có: \(\tan B = \dfrac{{AD}}{{BD}};\tan C = \dfrac{{AD}}{{CD}}\).

Suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{BD.CD}}\)   (1)

\(\widehat {HBD} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)); \(\widehat {HDB} = \widehat {ADC} = {90^0}\).

Do đó \(\Delta BDH \backsim \Delta ADC\) (g.g), suy ra \(\dfrac{{DH}}{{DC}} = \dfrac{{BD}}{{AD}}\), do đó \(BD.DC = DH.AD\)  (2).

Từ (1) và (2) suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{DH.AD}} = \dfrac{{AD}}{{DH}}\)  (3).

Theo giả thiết \(\dfrac{{HD}}{{AH}} = \dfrac{1}{2}\) suy ra \(\dfrac{{HD}}{{AH + HD}} = \dfrac{1}{{2 + 1}}\) hay \(\dfrac{{HD}}{{AD}} = \dfrac{1}{3}\), suy ra \(AD = 3HD\).

Thay vào (3) ta được: \(\tan B.\tan C = \dfrac{{3HD}}{{DH}} = 3\).

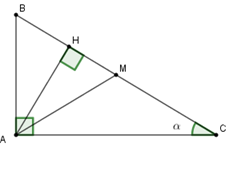
Góc \(2\alpha \) là góc \(AMH\).

+ Ta có \(BC = 2AM;\,AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}\)  nên \(\sin 2\alpha  = \sin \widehat {AMH} = \dfrac{{AH}}{{AM}} = \dfrac{{2AH}}{{BC}}\)\( = 2.\dfrac{{AB.AC}}{{B{C^2}}} = 2.\dfrac{{AB}}{{BC}}.\dfrac{{AC}}{{BC}}\)

Mà theo định nghĩa tỉ số lượng giác của góc nhọn ta có \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}}\)  nên

\(\sin 2\alpha  = 2.\sin \alpha .\cos \alpha \)  hay A đúng.

+)  Ta có \(\cos 2\alpha  = \cos \widehat {AMH} = \dfrac{{HM}}{{AM}}\)  (trong tam giác vuông \(AMH\) ) ; \(A{C^2} = HC.BC \Rightarrow HC = \dfrac{{A{C^2}}}{{BC}}\) và \(\cos \alpha  = \dfrac{{AC}}{{BC}}\)  nên

\(1 + \cos 2\alpha  = 1 + \dfrac{{HM}}{{AM}} = \dfrac{{AM + HM}}{{AM}} = \dfrac{{HM + MC}}{{AM}} = \dfrac{{HC}}{{AM}}\) \( = 2\dfrac{{HC}}{{BC}} = 2\dfrac{{A{C^2}}}{{B{C^2}}} = 2{\cos ^2}\alpha ;\)

Do đó B đúng.

+) \(1 - \cos 2\alpha  = 1 - \dfrac{{HM}}{{AM}} = \dfrac{{AM - HM}}{{AM}} = \dfrac{{HB}}{{AM}}\)\( = 2\dfrac{{HB}}{{BC}} = 2\dfrac{{A{B^2}}}{{B{C^2}}} = 2{\sin ^2}\alpha \)

Do đó C đúng.

Vậy cả A, B, C đều đúng.

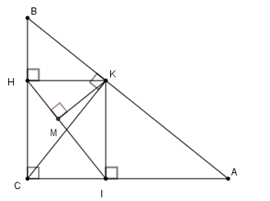
+) Xét tứ giác \(HKIC\) có \(\widehat C = \widehat I = \widehat H = 90^\circ \) nên tứ giác \(HKIC\)  là hình chữ nhật suy ra \(HK = CI;HC = IK;KC = HI\) .

+) Xét tam giác vuông \(KHI\)  có \(KM\) là chiều cao nên theo hệ thức lượng ta có\(\dfrac{1}{{K{M^2}}} = \dfrac{1}{{K{H^2}}} + \dfrac{1}{{K{I^2}}} = \dfrac{1}{{C{I^2}}} + \dfrac{1}{{H{C^2}}}\)  (vì \(HK = CI;HC = IK\)) nên A đúng.

+)  Xét tam giác vuông \(KAC\) , theo hệ thức lượng ta có \(K{A^2} = AI.AC \Rightarrow AI = \dfrac{{K{A^2}}}{{AC}}\)

Xét tam giác vuông \(KBC\) , theo hệ thức lượng ta có \(K{B^2} = BH.BC \Rightarrow BH = \dfrac{{K{B^2}}}{{BC}}\)

Lại có theo hệ thức lượng trong tam giác vuông \(ABC\) thì \(A{C^2} = AK.AB \Rightarrow KA = \dfrac{{A{C^2}}}{{AB}}\) ;

\(B{C^2} = KB.AB \Rightarrow KB = \dfrac{{B{C^2}}}{{AB}}\) .

Từ đó ta có \(\dfrac{{AI}}{{BH}} = \dfrac{{K{A^2}}}{{AC}}:\dfrac{{K{B^2}}}{{BC}}\) $ = \left( {\dfrac{{A{C^2}}}{{AB}}:\dfrac{{B{C^2}}}{{AB}}} \right)^2.\dfrac{{BC}}{{AC}}$ \( = {\left( {\dfrac{{AC}}{{BC}}} \right)^4}.\dfrac{{BC}}{{AC}} = {\left( {\dfrac{{AC}}{{BC}}} \right)^3}\)

Do đó B đúng.

Hay cả A, B đều đúng.

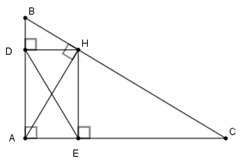
Tứ giác \(DAEH\) có \(\widehat D = \widehat A = \widehat E = 90^\circ \)  nên nó là hình chữ nhật suy ra \(AH = DE.\)

Theo hệ thức lượng trong các tam giác vuông \(AHB;\,AHC\)  ta có

\(H{B^2} = BD.AB \Rightarrow BD = \dfrac{{H{B^2}}}{{AB}}\) ; \(H{C^2} = CE.CA \Rightarrow CE = \dfrac{{H{C^2}}}{{AC}}\)  nên ta có

\(BD.CE.BC = \dfrac{{H{B^2}}}{{AB}}.\dfrac{{H{C^2}}}{{AC}}.BC\)

\( = {\left( {HB.HC} \right)^2}.\dfrac{{BC}}{{AB.AC}}\) mà \(HB.HC = A{H^2}\)  (hệ thức lượng trong tam giác vuông \(ABC\) )

\( = A{H^4}.\dfrac{1}{{AH}} = A{H^3} = D{E^3}\) (vì \(AH = DE\) (cmt))

Vậy $D{E^3} = BD.CE.BC$.

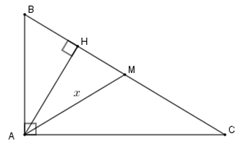
Đặt \(AM = x\,\left( {x > 0;cm} \right) \Rightarrow BC = 2x\,\left( {cm} \right);AH = x - 7\,\left( {cm} \right)\)

Vì chu vi tam giác \(ABC\) là \(72cm\) nên \(AB + AC + BC = 72 \Rightarrow AB + AC = 72 - 2x\,\left( {cm} \right)\)

Theo các hệ thức trong tam giác vuông:

\(A{B^2} + A{C^2} = B{C^2} = 4{x^2}\,\,\left( 1 \right)\) ; \(AB.AC = BC.AH = 2x\left( {x - 7} \right)\,\,\,\,\,\left( 2 \right)\)

Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(A{B^2} + A{C^2} + 2AB.AC = 4{x^2} + 4x\left( {x - 7} \right)\)

\( \Leftrightarrow {\left( {AB + AC} \right)^2} = 8{x^2} - 28x \Leftrightarrow {\left( {72 - 2x} \right)^2} = 8{x^2} - 28x\)

Đưa về phương trình \({x^2} + 65x - 1296 = 0 \Leftrightarrow \left( {x - 16} \right)\left( {x + 81} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\left( N \right)\\x =  - 81\,\,\left( L \right)\end{array} \right.\)

Từ đó \(BC = 32\,cm;\,AH = 9\,cm.\) Khi đó \({S_{ABC}} = \dfrac{1}{2}.32.9 = 144\,\,\left( {c{m^2}} \right)\)

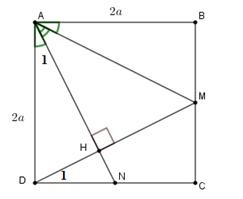
Gọi \(H\) là giao điểm của \(AN\)   và \(DM\).

Vì \(ABCD\) là hình vuông và \(M,N\)  theo thứ tự là trung điểm của \(BC;CD.\)

Nên \(AD = DC;\,DN = CM\)

Từ đó $\Delta ADN = \Delta DCM\,\left( {c.g.c} \right)$  nên \(\widehat {{A_1}} = \widehat {{D_1}} \Rightarrow AH \bot DM\)  (do $\widehat {{A_1}} + \widehat {AND} = 90^\circ  \Rightarrow \widehat {{D_1}} + \widehat {HND} = 90^\circ  \Rightarrow \widehat {DHN} = 90^\circ $ )

Suy ra \(\cos \widehat {MAN} = \dfrac{{AH}}{{AM}}\)

Đặt \(AB = AD = 2a\)  ta tính được \(AM = AN = a\sqrt 5 \)

Từ \(A{D^2} = AH.AN\)  ta có \(AH = \dfrac{{4a}}{{\sqrt 5 }}\) . Do đó

\(\cos \widehat {MAN} = \dfrac{{AH}}{{AM}} = \dfrac{{4a}}{{\sqrt 5 }}:\left( {a\sqrt 5 } \right) = \dfrac{4}{5}.\)