Cho tam giác $ABC$ vuông tại $A$,$AB < AC,\widehat C = \alpha  < {45^0}$, đường trung tuyến $AM$, đường cao $AH$, $MA = MB = MC = a.$ Chọn câu đúng.

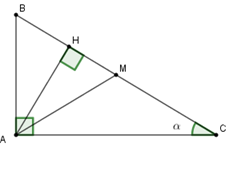
Góc $2\alpha$ là góc $AMH$.

+ Ta có $BC = 2AM;\,AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}$  nên $\sin 2\alpha  = \sin \widehat {AMH} = \dfrac{{AH}}{{AM}} = \dfrac{{2AH}}{{BC}}$$= 2.\dfrac{{AB.AC}}{{B{C^2}}} = 2.\dfrac{{AB}}{{BC}}.\dfrac{{AC}}{{BC}}$

Mà theo định nghĩa tỉ số lượng giác của góc nhọn ta có $\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}}$  nên

$\sin 2\alpha  = 2.\sin \alpha .\cos \alpha$  hay A đúng.

+)  Ta có $\cos 2\alpha  = \cos \widehat {AMH} = \dfrac{{HM}}{{AM}}$  (trong tam giác vuông $AMH$ ) ; $A{C^2} = HC.BC \Rightarrow HC = \dfrac{{A{C^2}}}{{BC}}$ và $\cos \alpha  = \dfrac{{AC}}{{BC}}$  nên

$1 + \cos 2\alpha  = 1 + \dfrac{{HM}}{{AM}} = \dfrac{{AM + HM}}{{AM}} = \dfrac{{HM + MC}}{{AM}} = \dfrac{{HC}}{{AM}}$ $= 2\dfrac{{HC}}{{BC}} = 2\dfrac{{A{C^2}}}{{B{C^2}}} = 2{\cos ^2}\alpha ;$

Do đó B đúng.

+) $1 - \cos 2\alpha  = 1 - \dfrac{{HM}}{{AM}} = \dfrac{{AM - HM}}{{AM}} = \dfrac{{HB}}{{AM}}$$= 2\dfrac{{HB}}{{BC}} = 2\dfrac{{A{B^2}}}{{B{C^2}}} = 2{\sin ^2}\alpha$

Do đó C đúng.

Vậy cả A, B, C đều đúng.