Tính diện tích một tam giác vuông có chu vi \(72\,cm\), hiệu giữa đường trung tuyến và đường cao ứng với cạnh huyền bằng \(7\,cm.\)

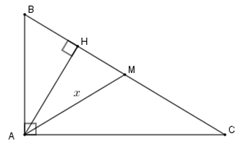
Đặt \(AM = x\,\left( {x > 0;cm} \right) \Rightarrow BC = 2x\,\left( {cm} \right);AH = x - 7\,\left( {cm} \right)\)

Vì chu vi tam giác \(ABC\) là \(72cm\) nên \(AB + AC + BC = 72 \Rightarrow AB + AC = 72 - 2x\,\left( {cm} \right)\)

Theo các hệ thức trong tam giác vuông:

\(A{B^2} + A{C^2} = B{C^2} = 4{x^2}\,\,\left( 1 \right)\) ; \(AB.AC = BC.AH = 2x\left( {x - 7} \right)\,\,\,\,\,\left( 2 \right)\)

Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(A{B^2} + A{C^2} + 2AB.AC = 4{x^2} + 4x\left( {x - 7} \right)\)

\( \Leftrightarrow {\left( {AB + AC} \right)^2} = 8{x^2} - 28x \Leftrightarrow {\left( {72 - 2x} \right)^2} = 8{x^2} - 28x\)

Đưa về phương trình \({x^2} + 65x - 1296 = 0 \Leftrightarrow \left( {x - 16} \right)\left( {x + 81} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\left( N \right)\\x =  - 81\,\,\left( L \right)\end{array} \right.\)

Từ đó \(BC = 32\,cm;\,AH = 9\,cm.\) Khi đó \({S_{ABC}} = \dfrac{1}{2}.32.9 = 144\,\,\left( {c{m^2}} \right)\)