Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB,{\rm{ }}AC.$ Chọn câu đúng.

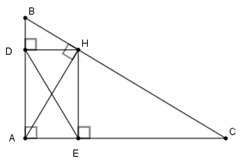
Tứ giác \(DAEH\) có \(\widehat D = \widehat A = \widehat E = 90^\circ \)  nên nó là hình chữ nhật suy ra \(AH = DE.\)

Theo hệ thức lượng trong các tam giác vuông \(AHB;\,AHC\)  ta có

\(H{B^2} = BD.AB \Rightarrow BD = \dfrac{{H{B^2}}}{{AB}}\) ; \(H{C^2} = CE.CA \Rightarrow CE = \dfrac{{H{C^2}}}{{AC}}\)  nên ta có

\(BD.CE.BC = \dfrac{{H{B^2}}}{{AB}}.\dfrac{{H{C^2}}}{{AC}}.BC\)

\( = {\left( {HB.HC} \right)^2}.\dfrac{{BC}}{{AB.AC}}\) mà \(HB.HC = A{H^2}\)  (hệ thức lượng trong tam giác vuông \(ABC\) )

\( = A{H^4}.\dfrac{1}{{AH}} = A{H^3} = D{E^3}\) (vì \(AH = DE\) (cmt))

Vậy $D{E^3} = BD.CE.BC$.