Cho hình vuông \(ABCD\). Tính \(\cos \,\widehat {MAN}\)  biết rằng \(M,N\)  theo thứ tự là trung điểm của \(BC;CD.\)

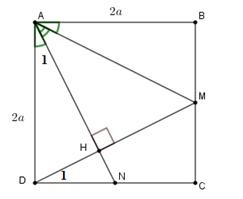
Gọi \(H\) là giao điểm của \(AN\)   và \(DM\).

Vì \(ABCD\) là hình vuông và \(M,N\)  theo thứ tự là trung điểm của \(BC;CD.\)

Nên \(AD = DC;\,DN = CM\)

Từ đó $\Delta ADN = \Delta DCM\,\left( {c.g.c} \right)$  nên \(\widehat {{A_1}} = \widehat {{D_1}} \Rightarrow AH \bot DM\)  (do $\widehat {{A_1}} + \widehat {AND} = 90^\circ  \Rightarrow \widehat {{D_1}} + \widehat {HND} = 90^\circ  \Rightarrow \widehat {DHN} = 90^\circ $ )

Suy ra \(\cos \widehat {MAN} = \dfrac{{AH}}{{AM}}\)

Đặt \(AB = AD = 2a\)  ta tính được \(AM = AN = a\sqrt 5 \)

Từ \(A{D^2} = AH.AN\)  ta có \(AH = \dfrac{{4a}}{{\sqrt 5 }}\) . Do đó

\(\cos \widehat {MAN} = \dfrac{{AH}}{{AM}} = \dfrac{{4a}}{{\sqrt 5 }}:\left( {a\sqrt 5 } \right) = \dfrac{4}{5}.\)