Cho tam giác $ABC$ vuông tại $C,$ đường cao $CK.$ Gọi \(H\)  và $I$ theo thứ tự là hình chiếu của K trên $BC$ và $AC.$ Gọi $M$ là chân đường vuông kẻ từ $K$ xuống $IH.$ Chọn câu đúng.

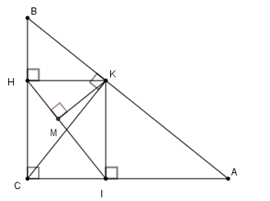
+) Xét tứ giác \(HKIC\) có \(\widehat C = \widehat I = \widehat H = 90^\circ \) nên tứ giác \(HKIC\)  là hình chữ nhật suy ra \(HK = CI;HC = IK;KC = HI\) .

+) Xét tam giác vuông \(KHI\)  có \(KM\) là chiều cao nên theo hệ thức lượng ta có\(\dfrac{1}{{K{M^2}}} = \dfrac{1}{{K{H^2}}} + \dfrac{1}{{K{I^2}}} = \dfrac{1}{{C{I^2}}} + \dfrac{1}{{H{C^2}}}\)  (vì \(HK = CI;HC = IK\)) nên A đúng.

+)  Xét tam giác vuông \(KAC\) , theo hệ thức lượng ta có \(K{A^2} = AI.AC \Rightarrow AI = \dfrac{{K{A^2}}}{{AC}}\)

Xét tam giác vuông \(KBC\) , theo hệ thức lượng ta có \(K{B^2} = BH.BC \Rightarrow BH = \dfrac{{K{B^2}}}{{BC}}\)

Lại có theo hệ thức lượng trong tam giác vuông \(ABC\) thì \(A{C^2} = AK.AB \Rightarrow KA = \dfrac{{A{C^2}}}{{AB}}\) ;

\(B{C^2} = KB.AB \Rightarrow KB = \dfrac{{B{C^2}}}{{AB}}\) .

Từ đó ta có \(\dfrac{{AI}}{{BH}} = \dfrac{{K{A^2}}}{{AC}}:\dfrac{{K{B^2}}}{{BC}}\) $ = \left( {\dfrac{{A{C^2}}}{{AB}}:\dfrac{{B{C^2}}}{{AB}}} \right)^2.\dfrac{{BC}}{{AC}}$ \( = {\left( {\dfrac{{AC}}{{BC}}} \right)^4}.\dfrac{{BC}}{{AC}} = {\left( {\dfrac{{AC}}{{BC}}} \right)^3}\)

Do đó B đúng.

Hay cả A, B đều đúng.