Câu hỏi:
2 năm trước
Trên các cạnh \(BC,CD\) của hình vuông \(ABCD\) ta lấy lần lượt các điểm \(M,N\) sao cho \(\widehat {MAN} = {45^0}\). Đường thẳng \(BD\) cắt các đường thẳng \(AM,AN\) tương ứng tại các điểm \(P,Q\).
Năm điểm nào sau đây cùng thuộc một đường tròn?
Trả lời bởi giáo viên
Đáp án đúng: b
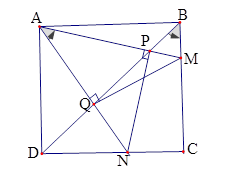
Từ kết quả câu trước ta suy ra \(\widehat {ADP} = \widehat {ANP} = {45^0},\widehat {QAM} = \widehat {QBM} = {45^0}\)\( \Rightarrow NP \bot AM,MQ \bot AN\). Tập hợp các điểm \(P,Q,C\) nhìn đoạn \(MN\) dưới một góc vuông, nên các điểm này nằm trên đường tròn đường kính \(MN\).
Hướng dẫn giải:
Sử dụng các đỉnh cùng nhìn cạnh \(AB\) dưới một góc vuông thì nằm trên đường tròn đường kính \(AB\)

