Cho nửa $(O)$ đường kính $AB.$ Lấy $M \in OA(M \ne O,A).$ Qua $M$ vẽ đường thẳng $d$ vuông góc với $AB.$ Trên $d$ lấy $N$ sao cho $ON > R.$ Nối $NB$ cắt $(O)$ tại $C.$ Kẻ tiếp tuyến $NE$ với $(O)$ ($E$ là tiếp điểm, $E$ và $A$ cùng thuộc nửa mặt phẳng bờ $d$). Gọi $H$ là giao điểm của $AC$ và $d$,  $F$ là giao điểm của $EH$ và đường tròn $(O)$. Chọn khẳng định sai?

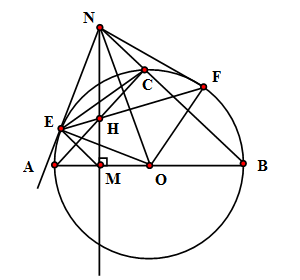
+) Vì \(\widehat {NEO} = \widehat {NMO} = 90^\circ  \Rightarrow NEMO\) là tứ giác nội tiếp nên bốn điểm $O,E,M,N$ cùng thuộc một đường tròn

\( \Rightarrow \) Phương án A đúng.

+) \(\widehat {NEC} = \widehat {CBE} = \dfrac{1}{2}\) số đo cung $CE \Rightarrow \Delta NEC\backsim\Delta NBE\left( {g - g} \right) \Rightarrow \dfrac{{NE}}{{NB}} = \dfrac{{NC}}{{NE}}$ \( \Rightarrow NB.NC = N{E^2}\)

\( \Rightarrow \) Phương án B đúng.

+) Hai tam giác vuông $\Delta NCH\backsim\Delta NMB\left( {g - g} \right) $

$\Rightarrow \dfrac{{NC}}{{NM}} = \dfrac{{NH}}{{NB}} $

$\Rightarrow NC.NB=NH.NM$

Từ đó $\Delta NEH\backsim\Delta NME\left( {c-g -c} \right) \Rightarrow \widehat {NEH} = \widehat {EMN}$ \( \Rightarrow \) Phương án C đúng.

+) \(\widehat {EMN} = \widehat {EON}\) (tứ giác \(NEMO\) nội tiếp) \( \Rightarrow \widehat {NEH} = \widehat {NOE}\) 

Mà góc $ENO$ phụ với góc $EON$ nên góc $ENO$ cũng phụ với góc $NEH$

\(\Rightarrow EH \bot NO\) 

\( \Rightarrow \Delta OEF\) cân có \(ON\) là phân giác

\( \Rightarrow \widehat {EON} = \widehat {NOF} \Rightarrow \widehat {NEF} = \widehat {NOF}\)  nên tứ giác \(NEOF\) nội tiếp \( \Rightarrow \widehat {NFO} = 180^\circ  - \widehat {NEO} = 90^\circ \) .

\( \Rightarrow \) Phương án D sai.