Trả lời bởi giáo viên
Đáp án đúng: b
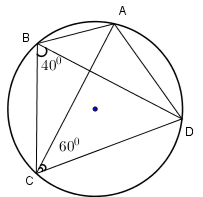
Do tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O,\) nên ta có
$\widehat {CAD} = \widehat {CBD}$ (cùng chắn cung \(CD\) ). Do đó ta có
\(\widehat {CAD} = {40^0}.\)
Tổng ba góc trong một tam giác bằng \({180^0}\)
Nên:
$\begin{array}{l}\widehat {CAD} + \widehat {ACD} + \widehat {ADC} = {180^0}\\ \Rightarrow \widehat {ADC} = {180^0} - \left( {\widehat {CAD} + \widehat {ACD}} \right) \\= {180^0} - \left( {{{40}^0} + {{60}^0}} \right) = {80^0}.\end{array}$
Hướng dẫn giải:
Sử dụng các tính chất:
- Góc nội tiếp cùng chắn một cung trong một đường tròn thì bằng nhau.
- Tổng ba góc trong một tam giác bằng \({180^0}\).
