Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {130^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), kẻ \(Bx \bot BA;Cy \bot CA\), \(Bx\) và \(Cy\) cắt nhau tại D. Chọn đáp án sai.
Trả lời bởi giáo viên
Đáp án đúng: c
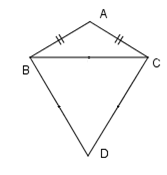
Theo đề bài ta có \(\widehat {ABD} = \widehat {ACD} = 90^\circ \Rightarrow \widehat {ABD} + \widehat {ACD} = 90^\circ + 90^\circ = 180^\circ \) mà hai góc \(\widehat {ABD};\widehat {ACD}\) ở vị trí đối nhau nên tứ giác \(ABDC\) là tứ giác nội tiếp nên đáp án B đúng.
+ Lại có \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = 130^\circ \Rightarrow \widehat {ABC} = \widehat {ACB} = \dfrac{{180^\circ - 130^\circ }}{2} = 25^\circ \)
+ Ta có \(\widehat {BDC} + \widehat {ABC} = 90^\circ \Rightarrow \widehat {BDC} = 90^\circ - 25^\circ = 65^\circ \)
Và \(\widehat {BCD} + \widehat {ACB} = 90^\circ \Rightarrow \widehat {BCD} = 90^\circ - 25^\circ = 65^\circ \)
Từ đó suy ra tam giác \(BCD\) cân tại \(D\) nên đáp án A đúng.
+ Xét tứ giác \(ABDC\) nội tiếp nên \(\widehat {BAC} + \widehat {BDC} = 180^\circ \Leftrightarrow \widehat {BDC} = 180^\circ - \widehat {BAC} = 180^\circ - 130^\circ = 50^\circ \) nên D đúng.
Ta chưa đủ điều kiện để suy ra tứ giác \(ABDC\) là hình thoi nên C sai.
Hướng dẫn giải:
Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
