Câu hỏi:
2 năm trước
Cho tứ giác ABCD nội tiếp (O) . M là điểm chính giữa cung AB. Nối M với D, M với C cắt AB lần lượt ở E và P. Trong các khẳng định sau, khẳng định nào đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
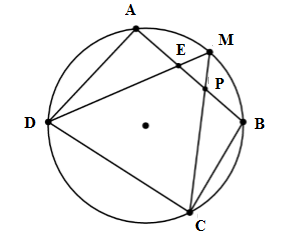
Theo đề bài ta có: M là điểm chính giữa cung AB nên \(\overparen {AM}=\overparen {MB}\)
Xét đường tròn (O) có:
+) \(\widehat {MCD}\) là góc nội tiếp chắn cung $DM \Rightarrow \widehat {MCD} = \dfrac{1}{2}sđ \overparen{DM}.\;\;\left( 1 \right)$
+) \(\widehat {AED}\) là góc có đỉnh nằm trong đường tròn chắn cung \(MB\) và cung \(AD\)
$ \Rightarrow \widehat {MCD} = \dfrac{1}{2}\left( {sđ \overparen{AD} + sđ \overparen{MB}} \right) $$= \dfrac{1}{2}\left( {sđ \overparen{AD} + sđ \overparen{MA}} \right) $$= \dfrac{1}{2}sđ \overparen{DM}\;\;\;\left( 2 \right)$
Từ (1) và (2) $ \Rightarrow \widehat {MCD} = \widehat {AED} $$= \dfrac{1}{2}sđ \overparen{DM}.$
Xét tứ giác DEPC có: \(\widehat {MCD} = \widehat {AED}\;\;\left( {cmt} \right)\)
$ \Rightarrow $PEDC nội tiếp (góc ngoài của một đỉnh bằng góc trong của đỉnh đối diện).
Hướng dẫn giải:
+) Sử dụng công thúc tính số đo góc có đỉnh nằm trong đường tròn
+) Nắm vững dấu hiêu chứng minh: Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện với đỉnh đó là tứ giác nội tiếp.
