Câu hỏi:
2 năm trước
Cho tam giác $ABC$ nhọn nội tiếp đường tròn$\left( O \right)$ . $M$ là điểm thuộc cung nhỏ $AC$ (cung \(CM < \) cung \(AM\) ). Vẽ $MH$ vuông góc với $BC$ tại $H$ , vẽ $MI$ vuông góc với $AC$ tại $I$ . Chọn câu đúng:
Trả lời bởi giáo viên
Đáp án đúng: d
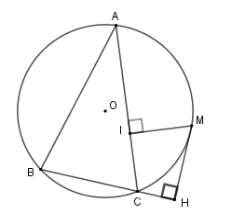
Xét tứ giác $IMHC$ ta có: $\widehat {MIC} = {90^0}$ ($MI$ vuông góc với$AC$ ); $\widehat {MHC} = {90^0}$($MH$ vuông góc với$BC$ )
$ \Rightarrow \widehat {{\rm{MIC}}} + \widehat {MHC} = {180^0}$ $ \Rightarrow $tứ giác $IMHC$ nội tiếp (dhnb).
Và tứ giác $IMHC$ chưa đủ điều kiện để là hình chữ nhật và hình vuông.
Hướng dẫn giải:
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
