Câu hỏi:
2 năm trước
Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(BC.\) Lấy điểm \(A\) trên tia đối của tia \(CB.\) Kẻ tiếp tuyến $AF,Bx$ của nửa đường tròn \(\left( O \right)\) (với \(F\) là tiếp điểm). Tia \(AF\) cắt tia \(Bx\) của nửa đường tròn tại \(D.\) Khi đó tứ giác \(OBDF\) là:
Trả lời bởi giáo viên
Đáp án đúng: b
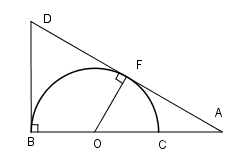
Ta có \(\widehat {DBO} = {90^0}\) và \(\widehat {DFO} = {90^0}\) ( tính chất tiếp tuyến).
Tứ giác \(OBDF\) có \(\widehat {DBO} + \widehat {DFO} = {90^0} + {90^0} = {180^0}\) nên nội tiếp được trong một đường tròn.
Hướng dẫn giải:
Tứ giác có tổng một cặp góc đối bằng \({180^0}\) là tứ giác nội tiếp.

