Câu hỏi:
2 năm trước
Cho tam giác ABC vuông tại A. Điểm E di động trên cạnh AB. Qua B vẽ một đường thẳng vuông góc cới CE tại D và cắt tia CA tại H. Biết $\widehat {BCA} = {30^0}.$ Số đo $\widehat {ADH}$ là:
Trả lời bởi giáo viên
Đáp án đúng: a
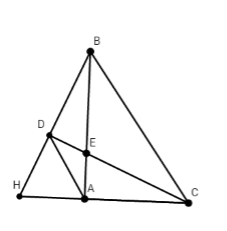
Xét tứ giác ACBD ta có:
$\widehat {BAC} = \widehat {BDC} = {90^0}$ và cùng nhìn đoạn BC.
\( \Rightarrow \) Tứ giác ACBD là tứ giác nội tiếp (dhnb).
$\begin{array}{l} \Rightarrow \widehat {BDA} + \widehat {BCA} = {180^ \circ }\\ \Leftrightarrow \widehat {BDA} = {180^0} - \widehat {BCA} = {180^0} - {30^0} = {150^0}.\end{array}$
Có góc $\widehat {HDA}$ và $\widehat {BDA}$ kề bù nên $\widehat {HDA} = {180^0} - \widehat {BDA} = {30^0}$
Hướng dẫn giải:
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Sử dụng tính chất trong tứ giác nội tiếp tổng hai góc đối diện bằng \({180^0}.\)
