Trả lời bởi giáo viên
Đáp án đúng: c
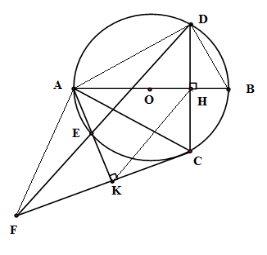
Xét \(\left( O \right)\) có \(\widehat {EAC} = \widehat {EDC}\) (hai góc nội tiếp cùng chắn một cung)
Xét tứ giác nội tiếp \(AHCK\) có \(\widehat {KAC} = \widehat {KHC}\) nên \(\widehat {EDC} = \widehat {KHC}\left( { = \widehat {KAC}} \right)\) mà hai góc ở vị trí đồng vị nên \(KH{\rm{//}}ED\)
Xét tam giác \(CFD\) có \(KH{\rm{//}}ED\)mà \(H\) là trung điểm của \(DC\) ( do \(AB \bot DC\)) nên \(K\) là trung điểm của \(CF\)
Xét tam giác \(ACF\) có \(AK\) vừa là đường trung tuyến vừa là đường cao nên \(\Delta ACF\) cân tại \(A\) .
Hướng dẫn giải:
Sử dụng tính chất tứ giác nội tiếp và góc nội tiếp để chứng minh các góc bằng nhau.

