Câu hỏi:
2 năm trước
Cho điểm A nằm ngoài đường tròn (O) qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm) . Chọn đáp án đúng:
Trả lời bởi giáo viên
Đáp án đúng: b
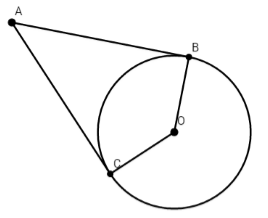
Ta có AB và AC là hai tiếp tuyến cắt nhau
\( \Rightarrow AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
Xét tứ giác ABOC có: $\left\{ \begin{array}{l}AB = AC\;\;\left( {cmt} \right)\\OB = OC\;\;\;\left( { = R} \right)\end{array} \right.$
$ \Rightarrow $ tứ giác ABOC chưa là hình thoi và không là hình bình hành.
$ \Rightarrow $đáp án A, D sai.
Có $\widehat {{\rm{ABO}}} = {90^0}$(do AB là tiếp tuyến của (O))
$\widehat {{\rm{ACO}}} = {90^0}$(do AC là tiếp tuyến của (O))
$ \Rightarrow \widehat {{\rm{ABO}}} + \widehat {ACO} = {180^0}$ $ \Rightarrow $tứ giác ABOC nội tiếp (dhnb).
\( \Rightarrow \) đáp án B đúng.
Hướng dẫn giải:
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
