Chọn câu sai.

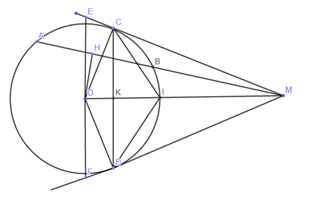
* Xét đường tròn $\left( {O;R} \right)$ có $H$ là trung điểm của dây cung $AB$$\Rightarrow OH \bot AB \Rightarrow \angle OHM = {90^o}$ (mối liên hệ giữa đường kính và dây cung)

Xét đường tròn $\left( {O;R} \right)$ có $MD$ là tiếp tuyến $\Rightarrow OD \bot MD \Rightarrow \angle ODM = {90^o}$ (tính chất của tiếp tuyến)

Xét tứ giác $DOHM$ có: $\left\{ \begin{array}{l}\angle OHM = {90^o}\\\angle ODM = {90^o}\end{array} \right. \Rightarrow \angle OHM + \angle ODM = {180^o}$

Suy ra tứ giác $DOHM$ nội tiếp đường tròn  $\Rightarrow D;O;H;M$ cùng thuộc một đường tròn nên A đúng.

* Xét $\Delta COM$ và $\Delta DOM$ có

+)$OM$ chung

+) $\angle OCM = \angle ODM = {90^o}$

+) $OC = OD = R$

$\Rightarrow \Delta COM = \Delta DOM$ (cạnh huyền - cạnh góc vuông) $\Rightarrow \angle COI = \angle IOD$ (2 góc tương ứng)

$\Rightarrow CI = ID \Rightarrow \Delta ICD$ cân $\Rightarrow \angle ICD = \angle IDC$ (Tính chất tam giác cân) 

Xét đường tròn $\left( {O;R} \right)$ có $\angle ICD$ là góc nội tiếp chắn cung $ID$; $\angle IDM$ là góc tạo bởi tiếp tuyến và dây cung chắn cung $ID$$\Rightarrow \angle ICD = \angle IDM$

Mà có $\angle ICD = \angle IDC \Rightarrow \angle IDO = \angle IDM$

$\Rightarrow ID$ là phân giác $\angle ODM$                                            (1)

Chứng minh tương tự có : $IC$ là phân giác $\angle MCO$  (2)

Mà có $ID$ cắt $IC$ tại $I$, suy ra $I$ là giao điểm của 3 đường phân giác trong $\Delta MCD$. Suy ra $I$ là tâm đường tròn nội tiếp $\Delta MCD$ nên B đúng, C sai.