Cho tam giác ABC cân tại A. Gọi I là tâm đường tròn nội tiếp tam giác, K là tâm đường tròn bàng tiếp góc A và O là trung điểm của IK.

Tính tổng diện tích các hình viên phân giới hạn bởi các cung nhỏ $CI,{\rm{ }}IB,{\rm{ }}BK,{\rm{ }}KC$ và các dây cung tương ứng của $\left( O \right)$ biết $AB = 20,{\rm{ }}BC = 24.$

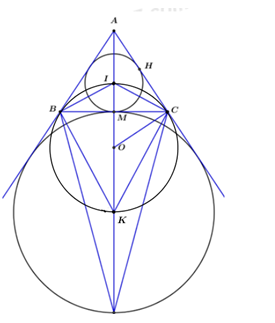
Gọi diện tích hình cần tính là S, diện tích hình tròn (O) là \(S'\) , gọi giao điểm $BC$ và $IK$ là $M.$

Ta có ngay :

$\begin{array}{l}S = S' - {S_{ICKB}} = \pi I{O^2} - {S_{IBK}} - {S_{IKC}}\\ = \pi \dfrac{{I{K^2}}}{4} - \dfrac{{BM.IK}}{2} - \dfrac{{CM.IK}}{2}\\ = \pi \dfrac{{I{K^2}}}{4} - \dfrac{{BC.IK}}{2}.\end{array}$

Ta có :

\(\begin{array}{l}\;\;\;\;\;{S_{ABC}} = \dfrac{1}{2}AM.BC = \dfrac{{AB + BC + CA}}{2}.IM\\ \Leftrightarrow \sqrt {A{B^2} - B{M^2}} .24 = \left( {AB + BC + CA} \right).IM\\ \Leftrightarrow \sqrt {{{20}^2} - {{\left( {\dfrac{{24}}{2}} \right)}^2}} .24 = \left( {20.2 + 24} \right).IM\\ \Leftrightarrow IM = 6.\end{array}\)

Áp dụng hệ thức lượng trong tam giác \(IBM\) vuông tại \(B\) có đường cao \(BM\) ta có :

\(\begin{array}{l}B{M^2} = IM.MK \Leftrightarrow MK = \dfrac{{B{M^2}}}{{IM}} = \dfrac{{{{12}^2}}}{6} = 24.\\ \Rightarrow IM = IM + MK = 6 + 24 = 30.\\ \Rightarrow S = \dfrac{1}{4}\pi I{K^2} - \dfrac{1}{2}BC.IK = \dfrac{1}{4}\pi {.30^2} - \dfrac{1}{2}.24.30\\ = 225\pi  - 360\;\;\left( {dvdt} \right).\end{array}\)