Giải tam giác vuông $ABC,$ biết $\widehat A = 90^\circ \;$ và $BC = 50cm;\widehat B = {48^o}$ (làm tròn đến chữ số thập phân thứ nhất)
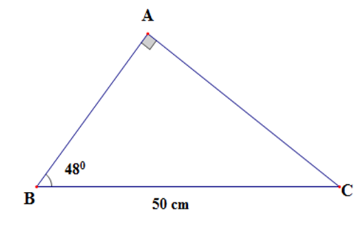
Xét $\Delta ABC$ có: $\widehat A = {90^o}$
$\widehat B + \widehat C = 90^\circ \Rightarrow \widehat C = 90^\circ - \widehat B = {90^o} - {48^o} = {42^o}$ ($\widehat C$ và $\widehat B$ là hai góc phụ nhau)
Áp dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông ta có:
\(AC = BC.\sin B = 50.\sin 48^\circ \approx 37,2cm\)
\(AB = BC.\cos B = 50.\cos 48^\circ \approx 33,5cm\)
Vậy \(AC = 37,2\,cm;\,AB = 33,5\,cm;\,\widehat C = 42^\circ \) .
Cho tam giác $ABC$ vuông tại $A$ có $AB = 21\,cm$; $\widehat C = 40^\circ $ , phân giác \(BD\) (\(D\) thuộc \(AC\) ). Độ dài phân giác $BD$ là (Kết quả làm tròn đến chữ số thập phân thứ nhất)
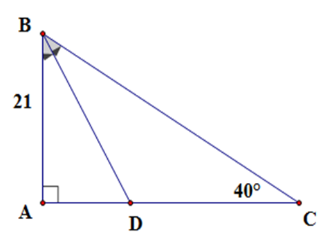
Xét tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} + \widehat C = 90^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Mà \(BD\) là phân giác góc \(ABC\) nên \(\widehat {ABD} = \dfrac{1}{2}\widehat {ABC} = 25^\circ \)
Xét tam giác \(ABD\) vuông tại \(A\) ta có \(BD = \dfrac{{AB}}{{\cos \widehat {ABD}}} = \dfrac{{21}}{{\cos 25^\circ }} \approx 23,2\,cm\)
Cho tam giác $ABC$ vuông tại $A,$ có $AC = 14,BC = 17.$ Khi đó \(\tan B\) bằng:
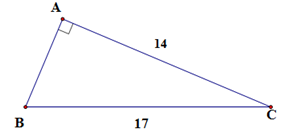
Xét tam giác \(ABC\) vuông tại \(A,\) theo định lý Pytago ta có \(A{B^2} + A{C^2} = B{C^2} \Rightarrow A{B^2} = {17^2} - {14^2} \Rightarrow AB = \sqrt {93} \)
Lại có $\tan B = \dfrac{{AC}}{{AB}} = \dfrac{{14}}{{\sqrt {93} }} = \dfrac{{14\sqrt {93} }}{{93}}$
Giá trị biểu thức ${\sin ^4}\alpha + {\cos ^4}\alpha + 2{\sin ^2}\alpha .{\cos ^2}\alpha $ là
Ta có ${\sin ^4}\alpha + {\cos ^4}\alpha + 2{\sin ^2}\alpha .{\cos ^2}\alpha $\( = {\left( {{{\sin }^2}\alpha } \right)^2} + 2{\sin ^2}\alpha .{\cos ^2}\alpha + {\left( {{{\cos }^2}\alpha } \right)^2}\) \( = {\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)^2} = {1^2} = 1\)
(vì \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\))
Cạnh bên của tam giác \(ABC\) cân tại \(A\) dài $20cm$ , góc ở đáy là \(50^\circ \)
Độ dài cạnh đáy của tam giác cân là (Kết quả làm tròn đến chữ số thập phân thứ nhất).
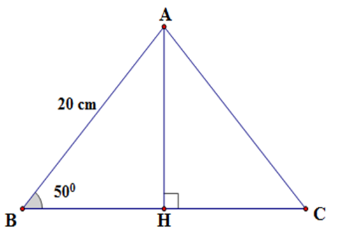
Kẻ \(AH \bot BC\) tại \(H.\) Suy ra \(H\) là trung điểm của \(BC\) (do tam giác \(ABC\) cân tại \(A\) có \(AH\) vừa là đường cao vừa là đường trung tuyến)
Xét tam giác \(AHB\) vuông tại \(H\) có \(\cos \widehat {ABH} = \dfrac{{BH}}{{AB}} \Rightarrow BH = AB.\cos \widehat {ABH}\)\( = 20.\cos 50^\circ \)
Mà \(H\) là trung điểm của \(BC\) nên \(BC = 2BH = 2.2.\cos 50^0\approx 25,7\,cm\)
Vậy \(BC \approx 25,7\,cm.\)
Cho hình vẽ, tìm \(x.\)
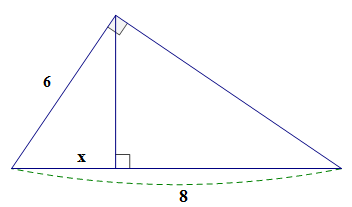
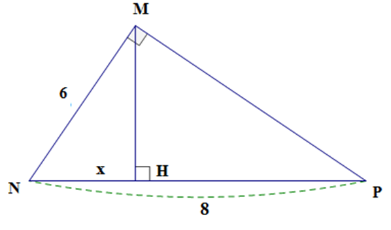
Đặt tên như hình vẽ trên.
Tam giác \(MNP\) vuông tại \(M\) có \(MH \bot NP\)
Theo hệ thức lượng trong tam giác vuông ta có \(M{N^2} = N{H^2}.NP \Rightarrow {6^2} = x.8 \Rightarrow x = 36:8 = 4,5.\)
Vậy \(x = 4,5.\)
Cho \(\tan \alpha = \dfrac{3}{4}\) . Giá trị biểu thức: \(M = \dfrac{{\sin \alpha - 2\cos \alpha }}{{\sin \alpha - \cos \alpha }}\)
Vì \(\tan \alpha = \dfrac{3}{4}\) nên \(\cos \alpha \ne 0.\) Chia cả tử và mẫu của \(M\) cho \(\cos \alpha \) ta được
\(M = \dfrac{{\left( {\sin \alpha - 2\cos \alpha } \right):\cos \alpha }}{{\left( {\sin \alpha - \cos \alpha } \right):\cos \alpha }}\) \( = \dfrac{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - 2}}{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - 1}} = \dfrac{{\tan \alpha - 2}}{{\tan \alpha - 1}}\)
Thay \(\tan \alpha = \dfrac{3}{4}\) vào \(M\) ta được \(M = \dfrac{{\dfrac{3}{4} - 2}}{{\dfrac{3}{4} - 1}} = 5.\)
Tìm \(x;y\) trong hình vẽ sau:
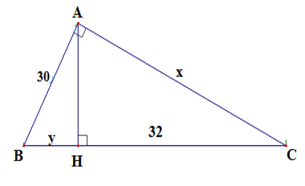
Ta có \(BC = BH + HC = y + 32\)
Áp dụng hệ thức lượng \(A{B^2} = BH.BC\) trong tam giác vuông \(ABC\) ta có
\(\begin{array}{l}{30^2} = y\left( {y + 32} \right)\\ \Leftrightarrow {y^2} + 32y - 900 = 0\\ \Leftrightarrow {y^2} + 50y - 18y - 90 = 0\\ \Leftrightarrow y\left( {y + 50} \right) - 18\left( {y + 50} \right) = 0\\ \Leftrightarrow \left( {y - 18} \right)\left( {y + 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}y - 18 = 0\\y + 50 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}y = 18\left( N \right)\\y = - 50\,\left( L \right)\end{array} \right.\end{array}\)
Suy ra \(y = 18 \Rightarrow BC = 18 + 32 = 50\)
Áp dụng hệ thức lượng \(A{C^2} = CH.BC\) ta có
\({x^2} = 32.50 \Leftrightarrow {x^2} = 1600 \Rightarrow x = 40.\)
Vậy \(x = 40;y = 18.\)
Tính số đo góc nhọn $x,$ biết: ${\cos ^2}x - {\sin ^2}x = \dfrac{1}{2}$
Ta có \({\sin ^2}x + {\cos ^2}x = 1\) \( \Rightarrow {\sin ^2}x = 1 - {\cos ^2}x\)
Từ đó ${\cos ^2}x - {\sin ^2}x = \dfrac{1}{2}$
\( \Leftrightarrow {\cos ^2}x - \left( {1 - {{\cos }^2}x} \right) = \dfrac{1}{2} \Leftrightarrow 2{\cos ^2}x = \dfrac{3}{2}\) \( \Leftrightarrow {\cos ^2}x = \dfrac{3}{4} \Rightarrow \cos x = \dfrac{{\sqrt 3 }}{2}\) (do \(x\) là góc nhọn nên \(\cos x > 0\) )
Suy ra \(x = 30^\circ .\)
Cho \(\Delta ABC\) vuông tại \(A.\) Biết $\dfrac{{AB}}{{AC}} = \dfrac{5}{7}$. Đường cao $AH = 15cm.$ Tính ${\rm{ }}HC.$
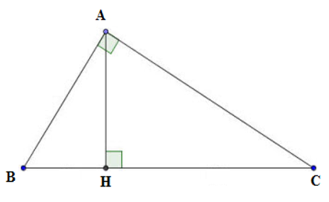
Vì \(\dfrac{{AB}}{{AC}} = \dfrac{5}{7} \Rightarrow AB = 5a;AC = 7a\) với \(a > 0.\)
Theo hệ thức lượng trong tam giác \(ABC\) vuông tại \(A\) ta có
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
\( \Leftrightarrow \dfrac{1}{{{{15}^2}}} = \dfrac{1}{{{{\left( {5a} \right)}^2}}} + \dfrac{1}{{{{\left( {7a} \right)}^2}}}\) \( \Leftrightarrow \dfrac{1}{{225}} = \dfrac{1}{{25{a^2}}} + \dfrac{1}{{49{a^2}}} \Leftrightarrow \dfrac{1}{{225}} = \dfrac{{74}}{{1225{a^2}}} \Rightarrow {a^2} = \dfrac{{666}}{{49}} \Rightarrow a = \dfrac{{3\sqrt {74} }}{7}\)
Suy ra \(AB = \dfrac{{15\sqrt {74} }}{7};AC = 3\sqrt {74} \)
Lại có \(AH.BC = AB.AC \Rightarrow BC = \dfrac{{AB.AC}}{{AH}} = \dfrac{{222}}{7}\)
Mà \(A{C^2} = CH.BC \Rightarrow HC = \dfrac{{A{C^2}}}{{BC}} = 21\,cm.\)
Cho \(\Delta ABC\) vuông tại $A,{\rm{ }}AB = {\rm{1}}2cm,{\rm{ }}AC = 16cm,$ tia phân giác $AD,$ đường cao $AH.$
Tính $HD.$
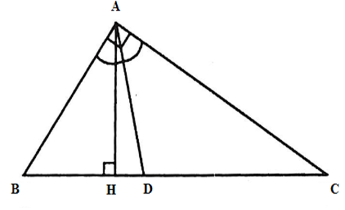
Xét tam giác vuông \(ABC\) ta có \(B{C^2} = A{B^2} + A{C^2}\) (định lý Pytago)
Hay \(B{C^2} = {12^2} + {16^2} \Rightarrow B{C^2} = 400 \Rightarrow BC = 20\,cm\)
Vì \(AD\) là phân giác góc \(A\) nên theo tính chất đường phân giác trong tam giác ta có
\(\dfrac{{BD}}{{AB}} = \dfrac{{DC}}{{AC}} \Leftrightarrow \dfrac{{BD}}{{12}} = \dfrac{{DC}}{{16}} = \dfrac{{BD + DC}}{{12 + 16}} = \dfrac{{BC}}{{28}} = \dfrac{{20}}{{28}} = \dfrac{5}{7}\)
Suy ra \(BD = 12.\dfrac{5}{7} = \dfrac{{60}}{7}\,cm\)
Theo hệ thức lượng trong tam giác vuông \(ABC\) ta có \(A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{{12}^2}}}{{20}} = 7,2\,cm\)
Lại có \(HD = BD - BH = \dfrac{{60}}{7} - 7,2 = \dfrac{{48}}{{35}}\,\,cm\)
Tính giá trị $C = {(3\sin \alpha + 4\cos \alpha )^2} + {\left( {4\sin \alpha - 3\cos \alpha } \right)^2}$
Ta có $C = {(3\sin \alpha + 4\cos \alpha )^2} + {\left( {4\sin \alpha - 3\cos \alpha } \right)^2}$\( = 9{\sin ^2}\alpha + 24\sin \alpha .\cos \alpha + 16{\cos ^2}\alpha + 16{\sin ^2}\alpha - 24\sin \alpha \cos \alpha + 9{\cos ^2}\alpha \)
\( = 25{\sin ^2}\alpha + 25{\cos ^2}\alpha = 25\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = 25.1 = 25\)
Vậy \(C = 25.\)
Cho biết $\tan \alpha = \dfrac{2}{3}$. Tính giá trị biểu thức: $M = \dfrac{{{{\sin }^3}\alpha + 3{{\cos }^3}\alpha }}{{27{{\sin }^3}\alpha - 25{{\cos }^3}\alpha }}$
Vì $\tan \alpha = \dfrac{2}{3}$ nên \(\cos \alpha \ne 0.\)
Chia cả tử và mẫu của $M$ cho $\cos^3 \alpha$ ta được
$M = \dfrac{{{{\sin }^3}\alpha + 3{{\cos }^3}\alpha }}{{27{{\sin }^3}\alpha - 25{{\cos }^3}\alpha }}$\( = \dfrac{{\dfrac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} + 3\dfrac{{{{\cos }^3}\alpha }}{{{{\cos }^3}\alpha }}}}{{27\dfrac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} - 25\dfrac{{{{\cos }^3}\alpha }}{{{{\cos }^3}\alpha }}}} = \dfrac{{{{\tan }^3}\alpha + 3}}{{27{{\tan }^3}\alpha - 25}}\)
Thay $\tan \alpha = \dfrac{2}{3}$ ta được \(M = \dfrac{{{{\left( {\dfrac{2}{3}} \right)}^3} + 3}}{{27.{{\left( {\dfrac{2}{3}} \right)}^3} - 25}} = \dfrac{{ - 89}}{{459}}.\)
Sắp xếp theo thứ tự tăng dần $\cot {70^0},{\rm{ tan}}\,{33^0},\cot {55^0},{\rm{ tan}}{28^0},{\rm{ cot}}{40^0}$
Ta có \(\cot 70^\circ = \tan 20^\circ \) vì \(70^\circ + 20^\circ = 90^\circ \) ; \(\cot \,55^\circ = \tan 35^\circ \,\,\) vì \(55^\circ + 35^\circ = 90^\circ \)
\(\cot 40^\circ = \tan 50^\circ \) vì \(40^\circ + 50^\circ = 90^\circ \)
Lại có \(20^\circ < 28^\circ < 33^\circ < 35^\circ < 50^\circ \) hay \(\tan 20^\circ < \tan 28^\circ < \tan 33^\circ < \tan 35^\circ < \tan 50^\circ \)
Suy ra \(\cot 70^\circ < \tan 28^\circ < \tan 33^\circ < \cot 55^\circ < \cot 40^\circ \)
Cho hình thang cân \(ABCD\,\,\,\left( {AB\parallel CD} \right);\) \(CD = 2AD = 2AB = 8\). Tính diện tích của hình thang đó.
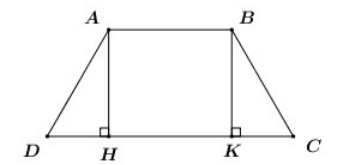
Kẻ \(AH,\,\,BK\) cùng vuông góc với \(CD\) \(\left( {H,\,\,K \in CD} \right)\).
Xét tứ giác \(ABKH\) có: \(\left\{ \begin{array}{l}AB\parallel HK\\AH\parallel BK\end{array} \right.\), suy ra \(ABKH\) là hình bình hành.
Lại có \(\angle AHK = {90^0}\) nên \(ABKH\) là hình chữ nhật, do đó \(HK = AB = 4\).
Xét \(\Delta ADH\) và \(\Delta BCK\) có:
\(\angle AHD = \angle BKC = {90^0}\);
\(AD = BC\) (tính chất hình thang cân);
\(\angle ADH = \angle ACK\) (tính chất hình thang cân).
\( \Rightarrow \Delta ADH = \Delta BCK\) (cạnh huyền – góc nhọn) \( \Rightarrow DH = CK\) (hai cạnh tương ứng).
Mà \(DH + CK = CD - HK = 8 - 4 = 4\).
Do đó \(DH = CK = 2\).
Áp dụng định lí Pytago trong tam giác vuông \(ADH\) ta có:
\(A{H^2} = A{D^2} - D{H^2}\) \( \Leftrightarrow A{H^2} = {4^2} - {2^2} = 12\) \( \Leftrightarrow AH = 2\sqrt 3 \).
Vậy diện tích hình thang \(ABCD\) là: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2}\) \( = \dfrac{{\left( {4 + 8} \right).2\sqrt 3 }}{2} = 12\sqrt 3 \).
Cho hình thang vuông \(ABCD\) có hai đáy \(AB = 12\,cm,\,\,DC = 16\,\,cm,\) cạnh xiên \(AD = 8\,cm.\) Tính các góc và cạnh góc vuông của hình thang.
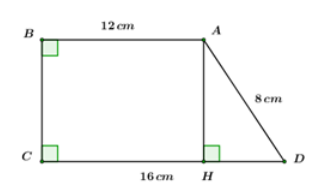
Kẻ \(AH \bot CD = \left\{ H \right\},\,\,H \in CD.\)
Có hình thang vuông \(ABCD\) cạnh xiên \(AD \Rightarrow \angle ABC = \angle BCD = {90^o}.\)
Dễ thấy \(ABCH\) là hình chữ nhật (có 3 góc vuông) \( \Rightarrow HC = AB = 12\,cm\)
\( \Rightarrow HD = DC - HC = 16 - 12 = 4\,\,(cm)\)
Áp dụng định lý Pitago cho \(\Delta AHD\) vuông tại \(H\) ta có:
\(\begin{array}{l}A{H^2} = A{D^2} - H{D^2} \Rightarrow AH = \sqrt {A{D^2} - H{D^2}} = \sqrt {{8^2} - {4^2}} = 4\sqrt 3 \,\,\left( {cm} \right).\\ \Rightarrow BC = AH \approx 6,93\,\,cm\end{array}\)
Xét \(\Delta AHD\) vuông tại \(H\) ta có: \(\cos \angle D = \dfrac{{HD}}{{AD}} = \dfrac{1}{2} \Rightarrow \angle D = {60^o}\)
\(\begin{array}{l} \Rightarrow \angle DAH = {90^o} - \angle D = {30^o}\\ \Rightarrow \angle BAD = \angle BAH + \angle DAH = {90^o} + {30^o} = {120^o}.\end{array}\)
Cho tứ giác \(ABCD\) có \(AB = AC = AD = 20\,\,cm,\,\,\angle B = {60^0}\) và \(\angle A = {90^0}.\) Kẻ \(BE \bot DC\) kéo dài.
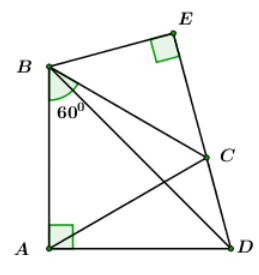
Tính \(BE\)?
Áp dụng định lý Pitago cho \(\Delta ABD\) vuông tại \(A\) ta có:
\(DB = \sqrt {A{B^2} + A{D^2}} = \sqrt {{{20}^2} + {{20}^2}} = 20\sqrt 2 \,\,cm.\)
Mà \(\Delta ABD\) có \(AB = AD = 20\,cm \Rightarrow \Delta ABD\) vuông cân tại\(A.\)
\( \Rightarrow \angle ABD = \angle ADB = {45^0}\) (tính chất tam giác cân).
Theo đề bài ta có: \(\left\{ \begin{array}{l}AB = AC = 20\,cm\\\angle ABC = {60^0}\end{array} \right. \Rightarrow \Delta ABC\) là tam giác đều.
\( \Rightarrow BC = 20\,cm;\,\,\,\angle BAC = \angle BCA = {60^0}.\)
Lại có: \(AC = AD = 20\,\,cm \Rightarrow \Delta ACD\) cân tại \(A\)
\(\begin{array}{l} \Rightarrow \angle ACD = \angle ADC = \dfrac{{{{180}^0} - \angle CAD}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - \angle BAC} \right)}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - {{60}^0}} \right)}}{2} = {75^0}.\\ \Rightarrow \angle EDB = \angle ADC - \angle ADB = {75^0} - {45^0} = {30^0}.\end{array}\)
Xét \(\Delta BED\) vuông tại \(E\) ta có:
\(\left\{ \begin{array}{l}BE = BD.\sin \angle EDB = 20\sqrt 2 .\sin {30^0} = 20\sqrt 2 .\dfrac{1}{2} = 10\sqrt 2 \,\,cm.\\ED = BD.cos\angle EDB = 20\sqrt 2 .cos{30^0} = 20\sqrt 2 .\dfrac{{\sqrt 3 }}{2} = 10\sqrt 6 \,\,cm.\end{array} \right.\)
Cho tứ giác \(ABCD\) có \(AB = AC = AD = 20\,\,cm,\,\,\angle B = {60^0}\) và \(\angle A = {90^0}.\) Kẻ \(BE \bot DC\) kéo dài.

Tính \(CE.\)?
Áp dụng định lý Pitago cho\(\Delta BEC\) vuông tại \(E\) ta có:
\(\begin{array}{l}EC = \sqrt {B{C^2} - B{E^2}} = \sqrt {{{20}^2} - {{\left( {10\sqrt 2 } \right)}^2}} \\ = 10\sqrt 2 \,\,cm.\end{array}\)
Cho tứ giác \(ABCD\) có \(AB = AC = AD = 20\,\,cm,\,\,\angle B = {60^0}\) và \(\angle A = {90^0}.\) Kẻ \(BE \bot DC\) kéo dài.

Tính \(CD\)?
Ta có: \( CD = ED - EC = 10\sqrt 6 - 10\sqrt 2 \)\(= 10\sqrt 2 \left( {\sqrt 3 - 1} \right)\,\,\,cm \approx 10,35\,\,cm\)
Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 15}}cm;AC = 20cm\). Phân giác của góc \(A\) cắt \(BC\) tại \(E\).
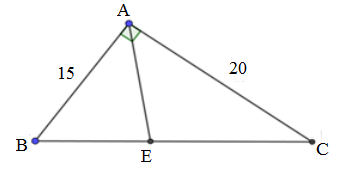
Giải tam giác \(ABC\)
Áp dụng định lý Pytago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {15^2} + {20^2} = 625\)\( \Rightarrow BC = 25\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{25}} \Rightarrow \angle B \approx {53^0}8'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {53^0}8' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {36^0}52'\)

