Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 15}}cm;AC = 20cm\). Phân giác của góc \(A\) cắt \(BC\) tại \(E\).
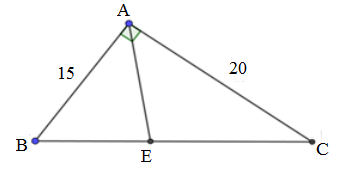
Tính \(BE;CE\).
Vì \(AE\) là tia phân giác góc \(A\) nên ta có:
\( \Rightarrow \dfrac{{BE}}{{AB}} = \dfrac{{EC}}{{AC}} = \dfrac{{BE + EC}}{{AB + AC}}\)\( = \dfrac{{BC}}{{AB + AC}} = \dfrac{{25}}{{15 + 20}} = \dfrac{5}{7}\)
\( \Rightarrow \left\{ \begin{array}{l}BE = \dfrac{5}{7}AB = \dfrac{5}{7}.15 = \dfrac{{75}}{7}\\EC = \dfrac{5}{7}AC = \dfrac{5}{7}.20 = \dfrac{{100}}{7}\end{array} \right..\)
Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là \({30^0}\), chiều dài mỗi bên dốc mái là \(3,5\,\,m.\) Tính gần đúng bề rộng của mái nhà.
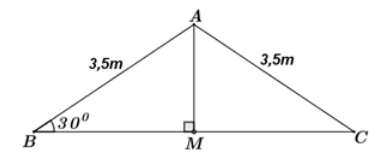
Ta vẽ lại mô hình mái nhà như hình vẽ bên.
Theo đề bài cho ta có: \(\Delta ABC\) cân tại \(A\)
\(AB = AC = 3,5m\) và \(\angle B = \angle C = {30^0}\)
Thì khi đó bề rộng mái nhà chính là độ dài cạnh \(BC.\)
Gọi \(M\) là trung điểm của \(BC.\)
\( \Rightarrow AM\) là đường trung tuyến đồng thời là đường cao của \(\Delta ABC\) (tính chất).
Xét \(\Delta ABM\) vuông tại \(M\) ta có:
\(\cos B = \dfrac{{BM}}{{AB}} \Rightarrow cos\,{30^0} = \dfrac{{BM}}{{3,5}} \Rightarrow BM = \cos \,{30^0}.3,5 = \dfrac{{\sqrt 3 }}{2}.3,5 = \dfrac{{7\sqrt 3 }}{4}\,\,\,\left( m \right).\)
\( \Rightarrow BC = 2BM\dfrac{{7\sqrt 3 }}{2}\,\,\left( m \right) \approx 6,06\,\,m.\)
Vậy bề rộng mái nhà là \(6,06\,m.\)
Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 6}}cm,{\rm{ }}AC{\rm{ }} = 4,5cm.\)
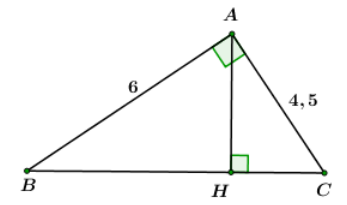
Tính các góc B, C và đường cao AH của tam giác.
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {6^2} + 4,{5^2} = 56,25\)\( \Rightarrow BC = 7,5\,\,cm.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \dfrac{{AC}}{{BC}} = \dfrac{{4,5}}{{7,5}} = \dfrac{3}{5} \Rightarrow \angle B \approx {36^0}52'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {36^0}52' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {53^0}8'\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,5 = 4,5.6\)\( \Leftrightarrow AH = 3,6\)
Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 6}}cm,{\rm{ }}AC{\rm{ }} = 4,5cm.\)

Tính diện tích của tam giác ABC.
Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}.AH.BC = \dfrac{1}{2}.3,6.7,5 = 13,5\,\,c{m^2}.\)
Cho tam giác \(ABC\) vuông tại \(A\),\(\angle B = {35^0}\)và \(AB{\rm{ }} = {\rm{ 6}}cm\). Vẽ đường cao \(AH\) và trung tuyến \(AM\) của tam giác \(ABC\).
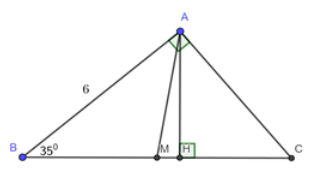
Giải tam giác vuông \(ABC\).
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = AB.tan\angle B = 6.tan{35^0} \approx 4,2\)
\(AB = BC.\cos \angle B \Rightarrow 6 = BC.\cos {35^0} \Rightarrow BC \approx 7,32\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {35^0} + \angle C = {90^0}\)\( \Leftrightarrow \angle C = {55^0}\)
Cho tam giác \(ABC\) vuông tại \(A\),\(\angle B = {35^0}\)và \(AB{\rm{ }} = {\rm{ 6}}cm\). Vẽ đường cao \(AH\) và trung tuyến \(AM\) của tam giác \(ABC\).

Tính diện tích \(\Delta AHM\)
Vì \(AM\) là trung tuyến của tam giác \(ABC \Rightarrow M\) là trung điểm \(BC\)\( \Rightarrow BM = MC = \dfrac{{BC}}{2} \approx 3,66\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A,\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,32 = 6.4,2\)\( \Leftrightarrow AH \approx 3,44\)
\(A{B^2} = BH.CB\)\( \Leftrightarrow {6^2} = BH.7,32\)\( \Leftrightarrow BH \approx 4,92\)
Ta có: \(BM + MH = BH \Leftrightarrow MH = 4,92 - 3,66 \approx 1,26\)
\({S_{\Delta AHM}} = \dfrac{1}{2}AH.MH \approx \dfrac{1}{2}.3,44.1,26 \approx 2,17\,\,\,\left( {đvdt} \right)\)
Cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\)và đường trung tuyến \(AM\). Biết \(AH = 3cm;\,HB = 4cm.\) Hãy tính \(AB,AC,AM\) và diện tích tam giác \(ABC.\)
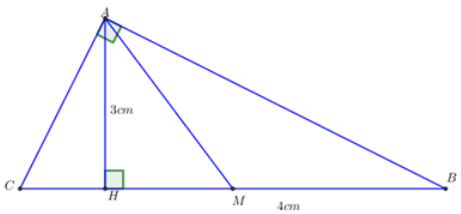
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(\,\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2} = {3^2} + {4^2} = 25 \Rightarrow AB = 5\,\,\,\left( {cm} \right)\).
+) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ABC với AH là đường cao ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{A{H^2}}} - \dfrac{1}{{A{B^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{3^2}}} - \dfrac{1}{{{5^2}}} = \dfrac{{16}}{{225}} \Rightarrow AC = \dfrac{{15}}{4}\left( {cm} \right)\)
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{15}}{4}} \right)^2} = \dfrac{{625}}{{16}} \Rightarrow BC = \dfrac{{25}}{4}\left( {cm} \right)\).
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có: \(AM = \dfrac{1}{2}BC = \dfrac{{25}}{8}\,\,\,\left( {cm} \right)\)
+) Diện tích tam giác ABC với AH là đường cao ta có: \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.3.\dfrac{{25}}{4} = \dfrac{{75}}{8}\,\,\left( {c{m^2}} \right)\).
Vậy \(AB = 5cm,\,\,AC = \dfrac{{15}}{4}cm,\,\,AM = \dfrac{{25}}{8}cm,\,\,{S_{\Delta ABC}} = \dfrac{{75}}{8}\,\,c{m^2}\)
Cho tam giác \(ABC\) có \(AB = 4cm,\,\,\,AC = 4\sqrt 3 ,\,\,BC = 8cm.\)
Tính số đo \(\angle B,\,\,\angle C\) và độ dài đường cao \(AH\) của \(\Delta ABC.\)
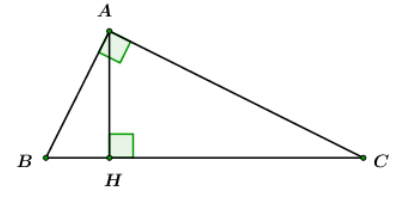
+) Chứng minh tam giác \(ABC\) vuông.
Ta có: \(A{B^2} = {4^2} = 16;\,\,A{C^2} = {\left( {4\sqrt 3 } \right)^2} = 48;\,\,B{C^2} = {8^2} = 64.\)
\( \Rightarrow A{B^2} + A{C^2} = 16 + 48 = 64 = B{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(A\) (định lý Pitago đảo).
+) Tính số đo \(\angle B,\,\,\angle C\) và độ dài đường cao \(AH\) của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong \(\Delta ABC\) ta có:
\(\begin{array}{l}\cos \angle B = \dfrac{{AB}}{{BC}} = \dfrac{4}{8} = \dfrac{1}{2} \Rightarrow \angle B = {60^0}\\ \Rightarrow \angle C = {180^0} - \angle B - \angle A = {180^0} - {60^0} - {90^0} = {30^0}.\end{array}\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại\(A\) và có đường cao \(AH\) ta có:
\(AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{4.4\sqrt 3 }}{8} = 2\sqrt 3 \,\,cm.\)
Vậy \(\angle B = {60^0},\,\,\,\angle C = {30^0},\,\,\,AH = 2\sqrt 3 \,\,cm.\)
Cho \(\Delta MNP\) vuông tại\(M\) có đường cao \(MH.\) Gọi \(I,\,\,K\) lần lượt là hình chiếu vuông góc của \(H\) trên \(MN,\,\,MP.\) Biết \(HK = 9\,cm,\,\,\,HI = 6\,cm.\) Khi đó tính độ dài các cạnh của \(\Delta MNP.\)
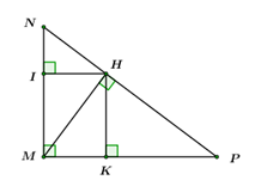
Xét tứ giác \(MIHK\) ta có: \(\angle M = \angle I = \angle K = {90^0}\)
\( \Rightarrow MIHK\) là hình chữ nhật (dhnb).
\( \Rightarrow HI = MK = 6\,cm.\)
Áp dụng định lý Pitago cho \(\Delta MHK\) vuông tại \(K\) ta có:
\(M{H^2} = H{K^2} + M{K^2} = {6^2} + {9^2} = 117 \Rightarrow MH = \sqrt {117} .\)
Áp dụng hệ thức lượng trong \(\Delta MHP\) vuông tại \(H\) có đường cao \(HK\) ta có:
\(M{H^2} = MK.MP \Rightarrow MP = \dfrac{{M{H^2}}}{{MK}} \)\(= \dfrac{{117}}{6} = 19,5\,cm.\)
Áp dụng hệ thức lượng trong \(\Delta MHN\) vuông tại \(H\) có đường cao \(HI\) ta có:
\(M{H^2} = MI.MN \Rightarrow MN = \dfrac{{M{H^2}}}{{MI}}\)\( = \dfrac{{117}}{9} = 13\,cm.\)
Áp dụng định lý Pitago cho \(\Delta MNP\) vuông tại \(N\) ta có:
\(NP = \sqrt {M{N^2} + M{P^2}} = \sqrt {{{13}^2} + 19,{5^2}}\)\( = \dfrac{{13\sqrt {13} }}{2}\,\,cm.\)
Vậy\(MN = 13\,\,cm,\,\,MP = 19,5\,\,cm,\,\,NP = \dfrac{{13\sqrt {13} }}{2}\,\,cm.\)
Cho đoạn thẳng $AB = 2a$ và trung điểm $O$ của nó. Trên nửa mặt phẳng bờ $AB$ vẽ các tia $Ax,By\;$ vuông góc với $AB.$ Qua \(O\) vẽ một tia cắt tia \(Ax\) tại $M$ sao cho $\widehat {AOM} = \alpha < {90^0}$ . Qua $O$ vẽ tia thứ hai cắt tia $By$ tại $N$ sao cho \(\widehat {MON} = 90^\circ \) . Khi đó, diện tích tam giác \(MON\) là
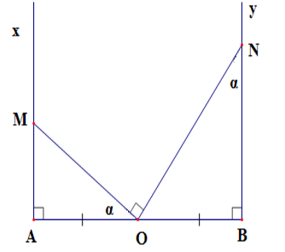
Theo đề bài ta có: \(AB = 2a \Rightarrow OA = OB = a\)
Ta có: \(\widehat {ONB} = \widehat {AOM} = \alpha \) (cùng phụ với \(\widehat {BON}\) )
Xét \(\Delta AOM\) có \(\widehat A = 90^\circ \)
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OA = OM.\cos \alpha \Rightarrow OM = \dfrac{a}{{\cos \alpha }}\)
Xét \(\Delta BON\) có \(\widehat B = 90^\circ \)
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OB = ON.\sin \alpha \Rightarrow ON = \dfrac{a}{{\sin \alpha }}\)
Vậy diện tích tam giác \(MON\) là: \(\dfrac{1}{2}OM.ON = \dfrac{1}{2}.\dfrac{a}{{\cos \alpha }}.\dfrac{a}{{\sin \alpha }} = \dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
Cho tam giác \(ABC\) có diện tích là \(900\,c{m^2}.\) Điểm \(D\) ở giữa \(BC\) sao cho \(BC = 5DC,\) điểm \(E\) ở giữa \(AC\) sao cho \(AC = 4AE,\) hai điểm \(F,G\) ở giữa \(BE\) sao cho \(BE = 6GF = 6GE.\) Tính diện tích tam giác \(DGF.\)
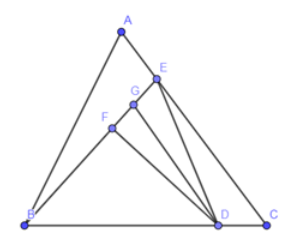
Ta kí hiệu: \(d(A;BC)\) là khoảng cách từ A đến đường thẳng BC (nghĩa là độ dài đoạn vuông góc kẻ từ A đến BC), tương tự với những kí hiệu khác trong bài.
Ta có: \(\left\{ \begin{array}{l}{S_{\Delta DFG}} = \dfrac{1}{2}d\left( {D;\,\,FG} \right).FG\\{S_{\Delta DEB}} = \dfrac{1}{2}d\left( {D;\,\,FG} \right).BE\end{array} \right. \Rightarrow \dfrac{{{S_{\Delta DFG}}}}{{{S_{\Delta DEB}}}} = \dfrac{{FG}}{{BE}} = \dfrac{1}{6}\) \( \Rightarrow {S_{\Delta DFG}} = \dfrac{1}{6}{S_{\Delta DEB}}.\)
\(\left\{ \begin{array}{l}{S_{\Delta DEB}} = \dfrac{1}{2}d\left( {D;\,\,BE} \right).BE\\{S_{\Delta BEC}} = \dfrac{1}{2}d\left( {C;\,\,BE} \right).BE\end{array} \right.\)\( \Rightarrow \dfrac{{{S_{\Delta DEB}}}}{{{S_{\Delta BEC}}}} = \dfrac{{d\left( {D;\,\,BE} \right)}}{{d\left( {C;\,\,BE} \right)}} = \dfrac{{BD}}{{BC}} = \dfrac{4}{5}\)\( \Rightarrow {S_{\Delta DEB}} = \dfrac{4}{5}{S_{\Delta BEC}}.\)
\(\left\{ \begin{array}{l}{S_{\Delta BEC}} = \dfrac{1}{2}d\left( {B;\,\,EC} \right).EC\\{S_{\Delta ABC}} = \dfrac{1}{2}d\left( {B;\,\,AC} \right).AC\end{array} \right.\) \( \Rightarrow \dfrac{{{S_{\Delta BEC}}}}{{{S_{\Delta ABC}}}} = \dfrac{{EC}}{{AC}} = \dfrac{3}{4}\)\( \Rightarrow {S_{\Delta BEC}} = \dfrac{3}{4}{S_{\Delta ABC}}.\)
\( \Rightarrow {S_{\Delta DFG}} = \dfrac{1}{6}.\dfrac{4}{5}.\dfrac{3}{4}.{S_{\Delta ABC}} = \dfrac{1}{{10}}.900 = 90\,c{m^2}.\)
Cho tam giác $ABC$ vuông tại $A$. Tính \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
Ta có: \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}}\)
\(\sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\;\)
\(\tan B = \dfrac{{AC}}{{AB}} \); \( \tan C = \dfrac{{AB}}{{AC}}\)
Vậy \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\;\)
\( = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1\)
\( = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0\) (vì theo định lý Pytago thì \(A{C^2} + A{B^2} = B{C^2}\) )

