Cho tam giác \(ABC\) có diện tích là \(900\,c{m^2}.\) Điểm \(D\) ở giữa \(BC\) sao cho \(BC = 5DC,\) điểm \(E\)  ở giữa \(AC\)  sao cho \(AC = 4AE,\) hai điểm \(F,G\) ở giữa \(BE\)  sao cho \(BE = 6GF = 6GE.\) Tính diện tích tam giác \(DGF.\) 

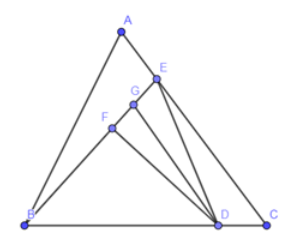
Ta kí hiệu: \(d(A;BC)\) là khoảng cách từ A đến đường thẳng BC (nghĩa là độ dài đoạn vuông góc kẻ từ A đến BC), tương tự với những kí hiệu khác trong bài.

Ta có: \(\left\{ \begin{array}{l}{S_{\Delta DFG}} = \dfrac{1}{2}d\left( {D;\,\,FG} \right).FG\\{S_{\Delta DEB}} = \dfrac{1}{2}d\left( {D;\,\,FG} \right).BE\end{array} \right. \Rightarrow \dfrac{{{S_{\Delta DFG}}}}{{{S_{\Delta DEB}}}} = \dfrac{{FG}}{{BE}} = \dfrac{1}{6}\) \( \Rightarrow {S_{\Delta DFG}} = \dfrac{1}{6}{S_{\Delta DEB}}.\)

\(\left\{ \begin{array}{l}{S_{\Delta DEB}} = \dfrac{1}{2}d\left( {D;\,\,BE} \right).BE\\{S_{\Delta BEC}} = \dfrac{1}{2}d\left( {C;\,\,BE} \right).BE\end{array} \right.\)\( \Rightarrow \dfrac{{{S_{\Delta DEB}}}}{{{S_{\Delta BEC}}}} = \dfrac{{d\left( {D;\,\,BE} \right)}}{{d\left( {C;\,\,BE} \right)}} = \dfrac{{BD}}{{BC}} = \dfrac{4}{5}\)\( \Rightarrow {S_{\Delta DEB}} = \dfrac{4}{5}{S_{\Delta BEC}}.\)

\(\left\{ \begin{array}{l}{S_{\Delta BEC}} = \dfrac{1}{2}d\left( {B;\,\,EC} \right).EC\\{S_{\Delta ABC}} = \dfrac{1}{2}d\left( {B;\,\,AC} \right).AC\end{array} \right.\) \( \Rightarrow \dfrac{{{S_{\Delta BEC}}}}{{{S_{\Delta ABC}}}} = \dfrac{{EC}}{{AC}} = \dfrac{3}{4}\)\( \Rightarrow {S_{\Delta BEC}} = \dfrac{3}{4}{S_{\Delta ABC}}.\)

 \( \Rightarrow {S_{\Delta DFG}} = \dfrac{1}{6}.\dfrac{4}{5}.\dfrac{3}{4}.{S_{\Delta ABC}} = \dfrac{1}{{10}}.900 = 90\,c{m^2}.\)