Cho tam giác \(ABC\) vuông tại \(A\),\(\angle B = {35^0}\)và \(AB{\rm{ }} = {\rm{ 6}}cm\). Vẽ đường cao \(AH\) và trung tuyến \(AM\) của tam giác \(ABC\).

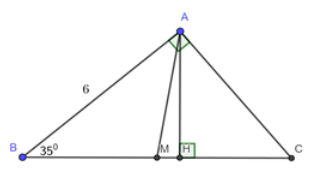
Tính diện tích \(\Delta AHM\)

Vì \(AM\) là trung tuyến của tam giác \(ABC \Rightarrow M\) là trung điểm \(BC\)\( \Rightarrow BM = MC = \dfrac{{BC}}{2} \approx 3,66\)

Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A,\) có đường cao \(AH\) ta có:

\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,32 = 6.4,2\)\( \Leftrightarrow AH \approx 3,44\)

\(A{B^2} = BH.CB\)\( \Leftrightarrow {6^2} = BH.7,32\)\( \Leftrightarrow BH \approx 4,92\)

Ta có: \(BM + MH = BH \Leftrightarrow MH = 4,92 - 3,66 \approx 1,26\)

\({S_{\Delta AHM}} = \dfrac{1}{2}AH.MH \approx \dfrac{1}{2}.3,44.1,26 \approx 2,17\,\,\,\left( {đvdt} \right)\)