Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\),\(\angle B = {35^0}\)và \(AB{\rm{ }} = {\rm{ 6}}cm\). Vẽ đường cao \(AH\) và trung tuyến \(AM\) của tam giác \(ABC\).
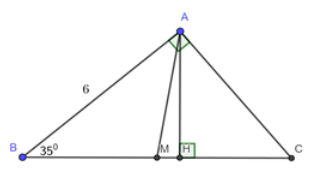
Giải tam giác vuông \(ABC\).
Trả lời bởi giáo viên
Đáp án đúng: c
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = AB.tan\angle B = 6.tan{35^0} \approx 4,2\)
\(AB = BC.\cos \angle B \Rightarrow 6 = BC.\cos {35^0} \Rightarrow BC \approx 7,32\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {35^0} + \angle C = {90^0}\)\( \Leftrightarrow \angle C = {55^0}\)
Hướng dẫn giải:
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông.
Sử dụng tính chất hai góc phụ nhau.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
