Cho \(\Delta MNP\) vuông tại\(M\) có đường cao \(MH.\) Gọi \(I,\,\,K\) lần lượt là hình chiếu vuông góc của \(H\) trên \(MN,\,\,MP.\) Biết \(HK = 9\,cm,\,\,\,HI = 6\,cm.\) Khi đó tính độ dài các cạnh của \(\Delta MNP.\)

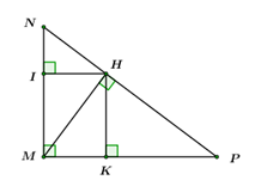
Xét tứ giác \(MIHK\) ta có: \(\angle M = \angle I = \angle K = {90^0}\)

\( \Rightarrow MIHK\) là hình chữ nhật (dhnb).

\( \Rightarrow HI = MK = 6\,cm.\)

Áp dụng định lý Pitago cho \(\Delta MHK\) vuông tại \(K\) ta có:

\(M{H^2} = H{K^2} + M{K^2} = {6^2} + {9^2} = 117 \Rightarrow MH = \sqrt {117} .\)

Áp dụng hệ thức lượng trong \(\Delta MHP\) vuông tại \(H\) có đường cao \(HK\)  ta có:

\(M{H^2} = MK.MP \Rightarrow MP = \dfrac{{M{H^2}}}{{MK}} \)\(= \dfrac{{117}}{6} = 19,5\,cm.\)

Áp dụng hệ thức lượng trong \(\Delta MHN\) vuông tại \(H\) có đường cao \(HI\)  ta có:

\(M{H^2} = MI.MN \Rightarrow MN = \dfrac{{M{H^2}}}{{MI}}\)\( = \dfrac{{117}}{9} = 13\,cm.\)

Áp dụng định lý Pitago cho \(\Delta MNP\) vuông tại \(N\) ta có:

\(NP = \sqrt {M{N^2} + M{P^2}}  = \sqrt {{{13}^2} + 19,{5^2}}\)\(  = \dfrac{{13\sqrt {13} }}{2}\,\,cm.\)

Vậy\(MN = 13\,\,cm,\,\,MP = 19,5\,\,cm,\,\,NP = \dfrac{{13\sqrt {13} }}{2}\,\,cm.\)