Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 6}}cm,{\rm{ }}AC{\rm{ }} = 4,5cm.\)

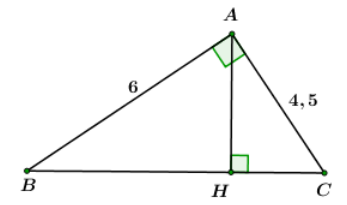
Tính các góc B, C và đường cao AH của tam giác.

Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:

\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {6^2} + 4,{5^2} = 56,25\)\( \Rightarrow BC = 7,5\,\,cm.\)

Xét \(\Delta ABC\) vuông tại \(A\)  ta có:

\(sinB = \dfrac{{AC}}{{BC}} = \dfrac{{4,5}}{{7,5}} = \dfrac{3}{5} \Rightarrow \angle B \approx {36^0}52'\)

Vì \(\Delta ABC\) vuông tại \(A\)  ta có:

\(\angle B + \angle C = {90^0} \Leftrightarrow {36^0}52' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {53^0}8'\)

Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:

\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,5 = 4,5.6\)\( \Leftrightarrow AH = 3,6\)