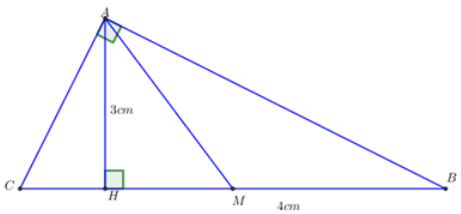
Cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\)và đường trung tuyến \(AM\). Biết \(AH = 3cm;\,HB = 4cm.\)  Hãy tính \(AB,AC,AM\) và diện tích tam giác \(ABC.\)

+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(\,\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2} = {3^2} + {4^2} = 25 \Rightarrow AB = 5\,\,\,\left( {cm} \right)\).
+) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ABC với AH là đường cao ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{A{H^2}}} - \dfrac{1}{{A{B^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{3^2}}} - \dfrac{1}{{{5^2}}} = \dfrac{{16}}{{225}} \Rightarrow AC = \dfrac{{15}}{4}\left( {cm} \right)\)
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{15}}{4}} \right)^2} = \dfrac{{625}}{{16}} \Rightarrow BC = \dfrac{{25}}{4}\left( {cm} \right)\).
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có: \(AM = \dfrac{1}{2}BC = \dfrac{{25}}{8}\,\,\,\left( {cm} \right)\)
+) Diện tích tam giác ABC với AH là đường cao ta có: \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.3.\dfrac{{25}}{4} = \dfrac{{75}}{8}\,\,\left( {c{m^2}} \right)\).
Vậy \(AB = 5cm,\,\,AC = \dfrac{{15}}{4}cm,\,\,AM = \dfrac{{25}}{8}cm,\,\,{S_{\Delta ABC}} = \dfrac{{75}}{8}\,\,c{m^2}\)