Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 15}}cm;AC = 20cm\). Phân giác của góc \(A\) cắt \(BC\) tại \(E\).
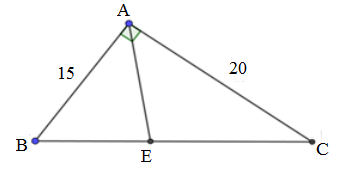
Tính \(BE;CE\).
Trả lời bởi giáo viên
Đáp án đúng: c
Vì \(AE\) là tia phân giác góc \(A\) nên ta có:
\( \Rightarrow \dfrac{{BE}}{{AB}} = \dfrac{{EC}}{{AC}} = \dfrac{{BE + EC}}{{AB + AC}}\)\( = \dfrac{{BC}}{{AB + AC}} = \dfrac{{25}}{{15 + 20}} = \dfrac{5}{7}\)
\( \Rightarrow \left\{ \begin{array}{l}BE = \dfrac{5}{7}AB = \dfrac{5}{7}.15 = \dfrac{{75}}{7}\\EC = \dfrac{5}{7}AC = \dfrac{5}{7}.20 = \dfrac{{100}}{7}\end{array} \right..\)
Hướng dẫn giải:
Sử dụng tính chất tia phân giác.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
