Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$. Tính \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
Trả lời bởi giáo viên
Đáp án đúng: a
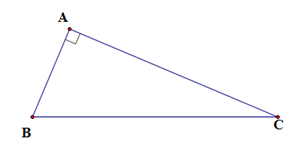
Ta có: \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}}\)
\(\sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\;\)
\(\tan B = \dfrac{{AC}}{{AB}} \); \( \tan C = \dfrac{{AB}}{{AC}}\)
Vậy \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\;\)
\( = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1\)
\( = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0\) (vì theo định lý Pytago thì \(A{C^2} + A{B^2} = B{C^2}\) )
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
