Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là \({30^0}\), chiều dài mỗi bên dốc mái là \(3,5\,\,m.\)  Tính gần đúng bề rộng của mái nhà.

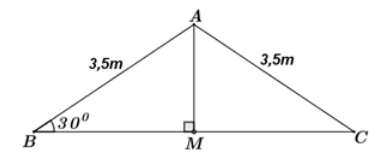
Ta vẽ lại mô hình mái nhà như hình vẽ bên.

Theo đề bài cho ta có: \(\Delta ABC\) cân tại \(A\)

\(AB = AC = 3,5m\) và \(\angle B = \angle C = {30^0}\)

Thì khi đó bề rộng mái nhà chính là độ dài cạnh \(BC.\)

Gọi \(M\)  là trung điểm của \(BC.\)

\( \Rightarrow AM\) là đường trung tuyến đồng thời là đường cao của \(\Delta ABC\) (tính chất).

Xét \(\Delta ABM\) vuông tại \(M\) ta có:

 \(\cos B = \dfrac{{BM}}{{AB}} \Rightarrow cos\,{30^0} = \dfrac{{BM}}{{3,5}} \Rightarrow BM = \cos \,{30^0}.3,5 = \dfrac{{\sqrt 3 }}{2}.3,5 = \dfrac{{7\sqrt 3 }}{4}\,\,\,\left( m \right).\)

\( \Rightarrow BC = 2BM\dfrac{{7\sqrt 3 }}{2}\,\,\left( m \right) \approx 6,06\,\,m.\)

Vậy bề rộng mái nhà là \(6,06\,m.\)