Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 15}}cm;AC = 20cm\). Phân giác của góc \(A\) cắt \(BC\) tại \(E\).
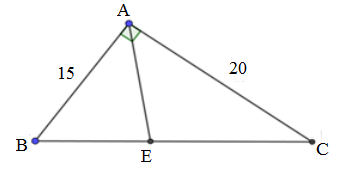
Giải tam giác \(ABC\)
Trả lời bởi giáo viên
Đáp án đúng: b
Áp dụng định lý Pytago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {15^2} + {20^2} = 625\)\( \Rightarrow BC = 25\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{25}} \Rightarrow \angle B \approx {53^0}8'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {53^0}8' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {36^0}52'\)
Hướng dẫn giải:
Sử dụng định lý Py-ta-go, tỉ số lượng giác của góc nhọn trong tam giác vuông.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
