Cho \(\Delta ABC\) vuông tại $A,{\rm{ }}AB = {\rm{1}}2cm,{\rm{ }}AC = 16cm,$ tia phân giác $AD,$ đường cao $AH.$
Tính $HD.$
Trả lời bởi giáo viên
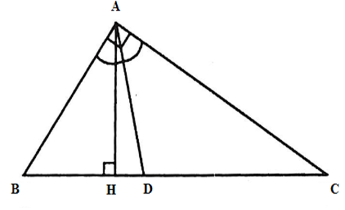
Xét tam giác vuông \(ABC\) ta có \(B{C^2} = A{B^2} + A{C^2}\) (định lý Pytago)
Hay \(B{C^2} = {12^2} + {16^2} \Rightarrow B{C^2} = 400 \Rightarrow BC = 20\,cm\)
Vì \(AD\) là phân giác góc \(A\) nên theo tính chất đường phân giác trong tam giác ta có
\(\dfrac{{BD}}{{AB}} = \dfrac{{DC}}{{AC}} \Leftrightarrow \dfrac{{BD}}{{12}} = \dfrac{{DC}}{{16}} = \dfrac{{BD + DC}}{{12 + 16}} = \dfrac{{BC}}{{28}} = \dfrac{{20}}{{28}} = \dfrac{5}{7}\)
Suy ra \(BD = 12.\dfrac{5}{7} = \dfrac{{60}}{7}\,cm\)
Theo hệ thức lượng trong tam giác vuông \(ABC\) ta có \(A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{{12}^2}}}{{20}} = 7,2\,cm\)
Lại có \(HD = BD - BH = \dfrac{{60}}{7} - 7,2 = \dfrac{{48}}{{35}}\,\,cm\)
Hướng dẫn giải:
Áp dụng tính chất đường phân giác của tam giác để tính \(BD.\)
Áp dụng hệ thức lượng trong tam giác vuông để tính \(BH\)
Từ đó tính \(HD.\)

