Cho \(\Delta ABC\) vuông tại  \(A.\) Biết $\dfrac{{AB}}{{AC}} = \dfrac{5}{7}$. Đường cao $AH = 15cm.$ Tính ${\rm{ }}HC.$

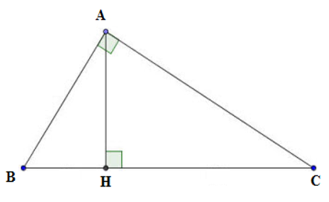
Vì \(\dfrac{{AB}}{{AC}} = \dfrac{5}{7} \Rightarrow AB = 5a;AC = 7a\)  với \(a > 0.\)

Theo hệ thức lượng trong tam giác \(ABC\) vuông tại \(A\) ta có

\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)

\( \Leftrightarrow \dfrac{1}{{{{15}^2}}} = \dfrac{1}{{{{\left( {5a} \right)}^2}}} + \dfrac{1}{{{{\left( {7a} \right)}^2}}}\) \( \Leftrightarrow \dfrac{1}{{225}} = \dfrac{1}{{25{a^2}}} + \dfrac{1}{{49{a^2}}} \Leftrightarrow \dfrac{1}{{225}} = \dfrac{{74}}{{1225{a^2}}} \Rightarrow {a^2} = \dfrac{{666}}{{49}} \Rightarrow a = \dfrac{{3\sqrt {74} }}{7}\)

Suy ra \(AB = \dfrac{{15\sqrt {74} }}{7};AC = 3\sqrt {74} \)

Lại có \(AH.BC = AB.AC \Rightarrow BC = \dfrac{{AB.AC}}{{AH}} = \dfrac{{222}}{7}\)

Mà \(A{C^2} = CH.BC \Rightarrow HC = \dfrac{{A{C^2}}}{{BC}} = 21\,cm.\)